题目内容
6.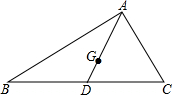 在Rt△ABC中,AD是斜边BC边上的中线,G是△ABC重心,如果BC=6,那么线段AG的长为2.
在Rt△ABC中,AD是斜边BC边上的中线,G是△ABC重心,如果BC=6,那么线段AG的长为2.
分析 根据直角三角形斜边上的中线性质得到AD=$\frac{1}{2}$BC=3,然后根据重心的性质得$\frac{AG}{GD}$=2,所以AG=$\frac{2}{3}$AD=2.
解答 解:∵AD是斜边BC边上的中线,
∴AD=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3,
∵G是△ABC重心,
∴$\frac{AG}{GD}$=2,
∴AG=$\frac{2}{3}$AD=$\frac{2}{3}$×3=2.
故答案为2.
点评 本题考查了三角形的重心:三角形的重心是三角形三边中线的交点;重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查了直角三角形斜边上的中线性质.

练习册系列答案
相关题目
1.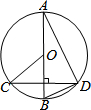 如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )
如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )
 如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )
如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )| A. | 25° | B. | 20° | C. | 65° | D. | 50° |
11.做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积的价格为b元,当造价最低时,锅炉的高与底面直径的比是( )
| A. | $\frac{a}{b}$ | B. | $\frac{{a}^{2}}{b}$ | C. | $\frac{b}{a}$ | D. | $\frac{{b}^{2}}{a}$ |
18.下列代数式中,次数为4的单项式是( )
| A. | x4+y4 | B. | xy2 | C. | 4xy | D. | x3y |
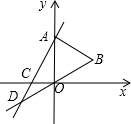 如图,点A的坐标为(0,2$\sqrt{3}$),△AOB是等边三角形,AC⊥AB,直线AC与x轴和直线OB分别相交于点C和点D,双曲线y=$\frac{k}{x}$经过点B.
如图,点A的坐标为(0,2$\sqrt{3}$),△AOB是等边三角形,AC⊥AB,直线AC与x轴和直线OB分别相交于点C和点D,双曲线y=$\frac{k}{x}$经过点B.