题目内容
17．解不等式组：$\left\{\begin{array}{l}{\frac{1-2x}{3}-\frac{4-3x}{6}≥\frac{x-2}{2}}\\{2x-7≤3（x-1）}\end{array}\right.$．分析 分别求出不等式组中两不等式的解集，找出两解集的公共部分即可．
解答 解：$\left\{\begin{array}{l}{\frac{1-2x}{3}-\frac{4-3x}{6}≥\frac{x-2}{2}①}\\{2x-7≤3（x-1）②}\end{array}\right.$，
由①得：x≤1，
由②得：x≥-4，
则不等式组的解集为-4≤x≤1．
点评 此题考查了解一元一次不等式组，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
7．某车间3月下旬生产零件的次品数如下（单位：个）：0，2，0，2，3，0，2，3，1，2，则在这10天中该车间生产的零件的次品数的（ ）
| A． | 众数是0 | B． | 极差是2 | C． | 平均数是2 | D． | 中位数是2 |
5．正八边形的中心角是（ ）
| A． | 45° | B． | 135° | C． | 360° | D． | 1080° |
12．
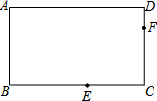在矩形ABCD中，点A关于角B的角平分线的对称点为E，点E关于角C的角平分线的对称点为F．若AD=$\sqrt{3}$AB=$\sqrt{3}$，则AF2=（ ）
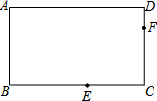在矩形ABCD中，点A关于角B的角平分线的对称点为E，点E关于角C的角平分线的对称点为F．若AD=$\sqrt{3}$AB=$\sqrt{3}$，则AF2=（ ）| A． | 8-4$\sqrt{3}$ | B． | 10-4$\sqrt{3}$ | C． | 8+4$\sqrt{3}$ | D． | 10+4$\sqrt{3}$ |
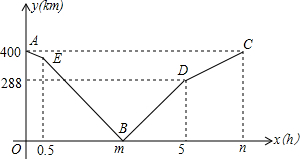甲乙两地相距400km，一辆轿车从甲地出发，以一定的速度匀速驶往乙地．0.5h后，一辆货车从乙地出发匀速驶往甲地（轿车的速度大于货车的速度），与轿车在途中相遇．此后，两车继续行驶，并各自到达目的地．两车之间的距离y（km）与轿车行驶的时间x（h）的函数图象如图．
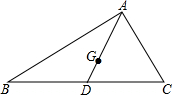在Rt△ABC中，AD是斜边BC边上的中线，G是△ABC重心，如果BC=6，那么线段AG的长为2．