题目内容
15.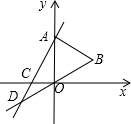 如图,点A的坐标为(0,2$\sqrt{3}$),△AOB是等边三角形,AC⊥AB,直线AC与x轴和直线OB分别相交于点C和点D,双曲线y=$\frac{k}{x}$经过点B.
如图,点A的坐标为(0,2$\sqrt{3}$),△AOB是等边三角形,AC⊥AB,直线AC与x轴和直线OB分别相交于点C和点D,双曲线y=$\frac{k}{x}$经过点B.(1)求k的值;
(2)判断点D是否在双曲线y=$\frac{k}{x}$上,并说明理由.
分析 (1)作BE⊥于x轴于E,由等边三角形的性质可知OA=OB=AB=2$\sqrt{3}$,∠AOB=∠ABO=∠BAO=60°,由∠AOC=90°=∠BAC得∠OAC=∠BOE=30°,通过解直角三角形求得;
(2)过D作DF⊥x轴于F 根据∠BAD=90°,∠B=60°,得出∠ADB=30°,从而得出∠ADO=∠OAD=30°,得出OD=OA=2$\sqrt{3}$,解30°角的直角三角形即可求得OF=3,DF=$\sqrt{3}$,求得D的坐标,代入反比例函数的解析式即可判断点D在双曲线y=$\frac{k}{x}$上.
解答 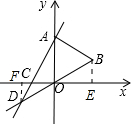 解:(1)作BE⊥于x轴于E,
解:(1)作BE⊥于x轴于E,
∵△AOB为等边三角形,A(0,2$\sqrt{3}$),
∴OA=OB=AB=2$\sqrt{3}$,∠AOB=∠ABO=∠BAO=60°,
∵∠AOC=90°=∠BAC,
∴∠OAC=∠BOE=30°,
∴OE=3,BE=$\sqrt{3}$,
∴B(3,$\sqrt{3}$),
∵双曲线y=$\frac{k}{x}$经过点B,
∴k=xy=3$\sqrt{3}$;
(2)D在双曲线y=$\frac{k}{x}$上;
理由:过D作DF⊥x轴于F
∵∠BAD=90°,∠B=60°,
∴∠ADB=30°,
∴∠ADO=∠OAD=30°
∴OD=OA=2$\sqrt{3}$,
又∵∠FOD=30°,
∴OF=3,DF=$\sqrt{3}$,
∴D(-3,-$\sqrt{3}$),
∵-3×(-$\sqrt{3}$)=3$\sqrt{3}$=k
∴D在双曲线y=$\frac{k}{x}$上.
点评 本题考查了反比例函数和一次函数的交点,等边三角形的性质,直角三角函数的应用,待定系数法求解析式等,作出辅助线构建直角三角形是解题的关键.

| A. | 45° | B. | 135° | C. | 360° | D. | 1080° |
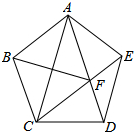 如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,已知AB=1,则DF的长是( )
如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,已知AB=1,则DF的长是( )| A. | $\frac{\sqrt{5}+1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
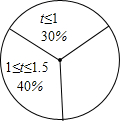 为了了解某初级中学800名学生完成课外作业所用的时间情况,从该校学生中随机抽取部分学生进行调查,按被调查学生完成课外作业时间t(小时)的人数分布,制成如图统计表和扇形统计图(均不完整)
为了了解某初级中学800名学生完成课外作业所用的时间情况,从该校学生中随机抽取部分学生进行调查,按被调查学生完成课外作业时间t(小时)的人数分布,制成如图统计表和扇形统计图(均不完整)| 时间t(小时) | t≤1 | 1<t≤1.5 | 1.5<t≤2 | t>2 |
| 人数(人) | 15 | 20 | 10 | 5 |
(1)抽样的学生数是50 人.在扇形统计图中,当1.5<t≤2时,
所对的圆心角的度数是72度;
(2)补全统计表与扇形统计图;
(3)若规定,初级中学学生完成课外作业时间不超过1.5小时.根据抽样情况,估计该校学生完成课外作业时间超过规定时间的学生人数.
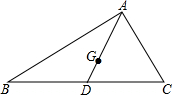 在Rt△ABC中,AD是斜边BC边上的中线,G是△ABC重心,如果BC=6,那么线段AG的长为2.
在Rt△ABC中,AD是斜边BC边上的中线,G是△ABC重心,如果BC=6,那么线段AG的长为2.