题目内容
 如图,小量角器的零度线在大量角器的零度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在小量角器上对应的度数为66°,那么在大量角器上对应的度数为
如图,小量角器的零度线在大量角器的零度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在小量角器上对应的度数为66°,那么在大量角器上对应的度数为考点:等腰三角形的性质,三角形内角和定理
专题:应用题
分析:依题意,设大量角器的左端点为A,小量角器的圆心为B.利用三角形的内角和定理求出∠PAB的度数.然后根据圆的知识可求出大量角器上对应的度数.
解答: 解:设大量角器的左端点是A,小量角器的圆心是B,连接AP,BP,
解:设大量角器的左端点是A,小量角器的圆心是B,连接AP,BP,
则∠APB=90°,∠ABP=66°,
因而∠PAB=90°-66°=24°,
在大量角器中弧PB所对的圆心角是48°,因而P在大量角器上对应的度数为48°.
故答案为:48.
 解:设大量角器的左端点是A,小量角器的圆心是B,连接AP,BP,
解:设大量角器的左端点是A,小量角器的圆心是B,连接AP,BP,则∠APB=90°,∠ABP=66°,
因而∠PAB=90°-66°=24°,
在大量角器中弧PB所对的圆心角是48°,因而P在大量角器上对应的度数为48°.
故答案为:48.
点评:本题主要考查了直径所对的圆周角是90度.能把实际问题转化为数学问题是解决本题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
函数y=x-
,则下列关于该函数的描述中,错误的是( )
| 1 |
| x |
| A、该函数的最小值是2 |
| B、该函数图象与y轴没有交点 |
| C、该函数图象与x轴有两个不同的交点 |
| D、当x>0时,y随着x的增大而增大 |
64的算术平方根是( )
| A、4 | B、±8 | C、-8 | D、8 |
在直角三角形ABC中,∠C=90°,a=6,b=8,则c=( )
| A、7 | B、8 | C、9 | D、10 |
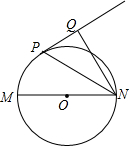 如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.
如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ. 如图,已知∠1=20°,∠2=25°,∠A=55°,求∠BDC的度数.
如图,已知∠1=20°,∠2=25°,∠A=55°,求∠BDC的度数.