Question

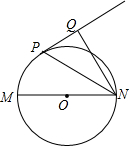如图，已知MN是⊙O的直径，直线PQ与⊙O相切于P点，NP平分∠MNQ．
（1）求证：NQ⊥PQ；
（2）若⊙O的半径R=3，∠MNP=30°，求NQ的长．

Answer 1

考点：切线的性质

专题：证明题

分析：（1）连结OP，如图，由NP平分∠MNQ得到∠1=∠3，加上∠1=∠2，则∠2=∠3，于是可判断OP∥NQ，再根据切线的性质得OP⊥PQ，所以NQ⊥PQ；
（2）连结MP，如图，根据圆周角定理，由MN是⊙O的直径，得到∠MPN=90°，在Rt△MPN中利用余弦的定义计算出PN=3

3

，然后在Rt△PNQ中，再次根据余弦的定义可计算出NQ．

解答：（1）证明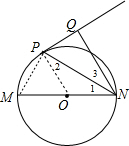：连结OP，如图，
∵NP平分∠MNQ，
∴∠1=∠3，
∵OP=ON，
∴∠1=∠2，
∴∠2=∠3，
∴OP∥NQ，
∵直线PQ与⊙O相切于P点，
∴OP⊥PQ，
∴NQ⊥PQ；
（2）解：连结MP，如图，
∵MN是⊙O的直径，
∴∠MPN=90°，
在Rt△MPN中，∵cos∠MNP=

PN

MN

，
∴PN=6cos30°=6×

3

2

=3

3

，
∵∠3=∠1=30°，
在Rt△PNQ中，∠3=∠1=30°，
∵cos∠3=

NQ

PN

，
∴NQ=3

3

cos30°=3

3

×

3

2

=

9

2

．

点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了矩形的性质和相似三角形的判定与性质．