题目内容
 如图,⊙O为Rt△ABC(∠ACB=90°)的内切圆,∠BOC=105°,AB=4 cm.
如图,⊙O为Rt△ABC(∠ACB=90°)的内切圆,∠BOC=105°,AB=4 cm.(1)∠A的度数;
(2)△ABC的面积.
考点:三角形的内切圆与内心
专题:计算题
分析:(1)根据三角形内切圆的定义得到OC平分∠ACB,OB平分∠ABC,则∠OCB=45°,再根据三角形内角和定理计算出∠OBC=180°-∠OCB-∠BOC=30°,所以∠ABC=2∠OBC=60°,然后利用互余可计算出∠A=30°;
(2)在Rt△ACB中,根据含30度的直角三角形三边的关系得到BC=
AB=2,AC=
BC=2
,然后利用三角形面积公式求解.
(2)在Rt△ACB中,根据含30度的直角三角形三边的关系得到BC=
| 1 |
| 2 |
| 3 |
| 3 |
解答:解:(1)∵⊙O为Rt△ABC(∠ACB=90°)的内切圆,
∴OC平分∠ACB,OB平分∠ABC,
∴∠OCB=
×90°=45°,
∴∠OBC=180°-∠OCB-∠BOC=180°-45°-105°=30°,
∴∠ABC=2∠OBC=60°,
∴∠A=90°-∠ABC=30°;
(2)在Rt△ACB中,∵∠A=30°,
∴BC=
AB=
×4=2,
∴AC=
BC=2
,
∴△ABC的面积=
•2•2
=2
(cm2).
∴OC平分∠ACB,OB平分∠ABC,
∴∠OCB=
| 1 |
| 2 |
∴∠OBC=180°-∠OCB-∠BOC=180°-45°-105°=30°,
∴∠ABC=2∠OBC=60°,
∴∠A=90°-∠ABC=30°;
(2)在Rt△ACB中,∵∠A=30°,
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AC=
| 3 |
| 3 |
∴△ABC的面积=
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
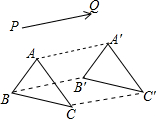 如图,△ABC沿PQ的方向平移到△A′B′C′的位置,AA′、BB′、CC′分别是对应点的连线,请问图中共有多少个平行四边形( )
如图,△ABC沿PQ的方向平移到△A′B′C′的位置,AA′、BB′、CC′分别是对应点的连线,请问图中共有多少个平行四边形( )| A、0个 | B、1个 | C、2个 | D、3个 |
 如图,已知直线y=
如图,已知直线y= 如图是李佳阳和蝴蝶夫人在做数学题时遇到的问题:已知矩形ABCD的顶点A在坐标原点,AB,AD分别在x轴,y轴的正半轴上,点B的坐标为(1,0),点D的坐标为(0,
如图是李佳阳和蝴蝶夫人在做数学题时遇到的问题:已知矩形ABCD的顶点A在坐标原点,AB,AD分别在x轴,y轴的正半轴上,点B的坐标为(1,0),点D的坐标为(0,
 如图,E是平行四边形ABCD的边AB延长线上一点,DE交BC于F,求证;S△ABF=S△EFC.
如图,E是平行四边形ABCD的边AB延长线上一点,DE交BC于F,求证;S△ABF=S△EFC.