Question

12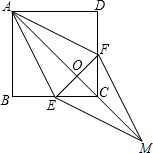．已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE=AF，连结AC交EF于点O，延长OC至点M，使OM=OA，连结EM，FM．
（1）判断四边形AEMF是什么特殊四边形？并证明你的结论；
（2）若正方形的边长为3cm，BE=DF=1cm，求四边形AEMF的面积．

Answer 1

分析 （1）用“HL”证明Rt△ABE和Rt△ADF全等，根据全等三角形对应边相等可得BE=DF，求出CE=CF，再判断AEMF是平行四边形，再结合AM⊥EF即可得到结论；
（2）利用勾股定理求出AE和EF的长度，进而求出AM的长，最后根据菱形的面积公式求出答案．

解答 （1）解：四边形AEMF是菱形．
∵四边形ABCD是正方形，
∴∠B=∠D=90°，AB=AD，
∵AE=AF，
∴Rt△ABE≌Rt△ADF （HL），
∴BE=DF，
∵在正方形ABCD中，∠1=∠2，BC=DC，

∴CE=CF，
∴AC⊥EF，且EO=FO，
∵OM=OA，
∴四边形AEMF是平行四边形，
又∵AM⊥EF，
∴平行四边形AEMF是菱形．
（2）解：∵AB=BC=DC=3，BE=DF=1，
∴CE=CF=2，
∴在Rt△ABE中，AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{10}$，
在Rt△ABE中，EF=$\sqrt{C{E}^{2}+C{F}^{2}}$=2$\sqrt{2}$，
∵四边形AEMF是菱形，
∴EO=$\sqrt{2}$，且EO⊥AO，
∴AO=$\sqrt{A{E}^{2}-E{O}^{2}}$=2$\sqrt{2}$，
∴AM=4$\sqrt{2}$，
∴菱形AEMF的面积为：S=$\frac{1}{2}$EF•AM=$\frac{1}{2}$×2$\sqrt{2}$×4$\sqrt{2}$=8（cm²）．

点评 本题主要考查对正方形的性质，平行四边形的判定，菱形的判定，全等三角形的性质和判定等知识点的理解和掌握，能综合运用这些性质进行推理是解此题的关键．