题目内容
17. (1)已知x,y满足二元一次方程组$\left\{\begin{array}{l}{2x+y=2}\\{x+2y=10}\end{array}\right.$,求x-y的值.
(1)已知x,y满足二元一次方程组$\left\{\begin{array}{l}{2x+y=2}\\{x+2y=10}\end{array}\right.$,求x-y的值.(2)如图,在△ABC中,∠B+∠C=110°,AD平分∠BAC,交BC于点D,DE∥AB,交AC于点E,求∠ADE的度数.
分析 (1)利用加减法求出方程组的解,代入x-y,计算即可求出其值;
(2)根据三角形的内角和得到∠BAC=70°,根据角平分线的定义得到∠BAD=$\frac{1}{2}$∠BAC=35°,根据平行线的性质即可得到结论.
解答 解:(1)$\left\{\begin{array}{l}{2x+y=2\\;①}\\{x+2y=10\\;②}\end{array}\right.$,
②×2-①,得3y=18,
解得y=6,
把y=6代入②,得x+12=10,
解得x=-2,
所以原方程组的解为$\left\{\begin{array}{l}{x=-2}\\{y=6}\end{array}\right.$,
则x-y=-2-6=-8;
(2)∵∠B+∠C=110°,
∴∠BAC=70°,
∵AD平分∠BAC,
∴∠BAD=$\frac{1}{2}$∠BAC=35°,
∵DE∥AB,
∴∠ADE=∠BAD=35°.
点评 本题考查了平行线的性质,三角形的内角和,二元一次方程组的解法以及代数式求值,正确求出x与y的值是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 如图,在Rt△ABC中,∠ABC=90°,点F在CB的延长线上且AB=BF,过F作EF⊥AC交AB于D,求证:DB=BC.
如图,在Rt△ABC中,∠ABC=90°,点F在CB的延长线上且AB=BF,过F作EF⊥AC交AB于D,求证:DB=BC.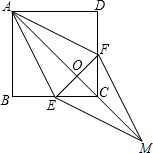 已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF,连结AC交EF于点O,延长OC至点M,使OM=OA,连结EM,FM.
已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF,连结AC交EF于点O,延长OC至点M,使OM=OA,连结EM,FM. 如图,等腰直角三角形ABC的斜边上取两点M,N,使∠MCN=45°,设AM=a,MN=x,BN=b,请判断以x,a,b为边长的三角形的形状.
如图,等腰直角三角形ABC的斜边上取两点M,N,使∠MCN=45°,设AM=a,MN=x,BN=b,请判断以x,a,b为边长的三角形的形状. 已知:Rt△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,BC交⊙O于E.
已知:Rt△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,BC交⊙O于E. 如图,在正方形ABCD中,E为BC的中点,F是CD上一点,且∠AEF=90°,求证:CF=$\frac{1}{4}$AB.
如图,在正方形ABCD中,E为BC的中点,F是CD上一点,且∠AEF=90°,求证:CF=$\frac{1}{4}$AB.