题目内容
2.已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”,试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系∠A+∠D=∠C+∠B;;
(2)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,利用(1)的结论,试求∠P的度数;
(3)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系?并说明理由.

分析 (1)∠A、∠B、∠C、∠D所在的两个三角形中,有一对对顶角相等,根据三角形的内角和定理得出数量关系;
(2)先根据“8字形”中的角的规律,可得∠DAP+∠D=∠P+∠DCP①,∠PCB+∠B=∠PAB+∠P②,再根据角平分线的定义,得出∠DAP=∠PAB,∠DCP=∠PCB,将①+②,可得2∠P=∠D+∠B,进而求出∠P的度数;
(3)根据(2)中的方法,即可求得∠P与∠D、∠B之间存在的数量关系.
解答 解:(1)根据三角形内角和定理以及对顶角相等,可得结论:∠A+∠D=∠C+∠B;
故答案为:∠A+∠D=∠C+∠B;
(2) 由(1)可知,∠1+∠D=∠P+∠3,①
由(1)可知,∠1+∠D=∠P+∠3,①
∠4+∠B=∠2+∠P,②
∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠1=∠2,∠3=∠4,
由①+②得:∠1+∠D+∠4+∠B=∠P+∠3+∠2+∠P,
即2∠P=∠D+∠B,
又∵∠D=40°,∠B=36°,
∴2∠P=40°+36°=76°,
∴∠P=38°;
(3)∠P与∠D、∠B之间存在的关系为2∠P=∠D+∠B.
∵∠1+∠D=∠P+∠3,①
∠4+∠B=∠2+∠P,②
∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠1=∠2,∠3=∠4,
由①+②得:∠1+∠D+∠4+∠B=∠P+∠3+∠2+∠P,
即2∠P=∠D+∠B.
点评 本题主要考查了三角形内角和定理,以及角平分线的定义,考核了学生的阅读理解与知识的迁移能力.解决问题的关键是根据三角形内角和定理得出“8字形”中的角的规律,以及直接运用“8字形”中的角的规律解题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
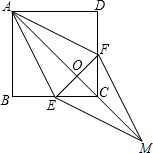 已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF,连结AC交EF于点O,延长OC至点M,使OM=OA,连结EM,FM.
已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF,连结AC交EF于点O,延长OC至点M,使OM=OA,连结EM,FM. 如图,平面直角坐标系中,△AOB的顶点均在边长为1的正方形在顶点上.
如图,平面直角坐标系中,△AOB的顶点均在边长为1的正方形在顶点上. 如图,E,F分别是正方形ABCD中BC和CD边上的点,且AB=4,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF,AE,求证:∠AFE=90°.
如图,E,F分别是正方形ABCD中BC和CD边上的点,且AB=4,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF,AE,求证:∠AFE=90°. 如图,在正方形ABCD中,E为BC的中点,F是CD上一点,且∠AEF=90°,求证:CF=$\frac{1}{4}$AB.
如图,在正方形ABCD中,E为BC的中点,F是CD上一点,且∠AEF=90°,求证:CF=$\frac{1}{4}$AB.
