题目内容
 如图所示,直线EF上有两点A,C,分别引两条射线AB,CD,∠BAF=110°,∠DCF=60°,射线AB,CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t,在射线CD移动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.
如图所示,直线EF上有两点A,C,分别引两条射线AB,CD,∠BAF=110°,∠DCF=60°,射线AB,CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t,在射线CD移动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.考点:平行线的判定
专题:
分析:分①AB与CD在EF的两侧,分别表示出∠ACD与∠BAC,然后根据内错角相等两直线平行,列式计算即可得解;
②CD旋转到与AB都在EF的右侧,分别表示出∠DCF与∠BAC,然后根据同位角相等两直线平行,列式计算即可得解;
③CD旋转到与AB都在EF的左侧,分别表示出∠DCF与∠BAC,然后根据同位角相等两直线平行,列式计算即可得解.
②CD旋转到与AB都在EF的右侧,分别表示出∠DCF与∠BAC,然后根据同位角相等两直线平行,列式计算即可得解;
③CD旋转到与AB都在EF的左侧,分别表示出∠DCF与∠BAC,然后根据同位角相等两直线平行,列式计算即可得解.
解答: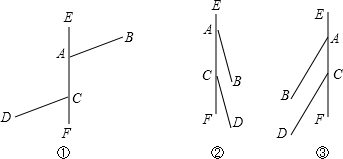 解:存在.分三种情况:
解:存在.分三种情况:
如图①,AB与CD在EF的两侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠ACD=180°-60°-3t=120°-3t,∠BAC=110°-t,
要使AB∥CD,则∠ACD=∠BAF,
即120°-3t=110°-t,
解得t=5;
此时(180°-60°)÷3=40,
∴0<t<40;
②CD旋转到与AB都在EF的右侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠DCF=360°-3t-60°=300°-3t,∠BAC=110°-t,
要使AB∥CD,则∠DCF=∠BAC,
即300°-3t=110°-t,
解得t=95°,
此时(360°-60°)÷3=100,
∴40<t<100;
③CD旋转到与AB都在EF的左侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠DCF=3t-(180°-60°+180°)=3t-300°,∠BAC=t-110°,
要使AB∥CD,则∠DCF=∠BAC,
即3t-300°=t-110°,
解得t=95°,
此时t>110,
∵95<110,
∴此情况不存在.
综上所述,t为5秒或95秒时,CD与AB平行.
 解:存在.分三种情况:
解:存在.分三种情况:如图①,AB与CD在EF的两侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠ACD=180°-60°-3t=120°-3t,∠BAC=110°-t,
要使AB∥CD,则∠ACD=∠BAF,
即120°-3t=110°-t,
解得t=5;
此时(180°-60°)÷3=40,
∴0<t<40;
②CD旋转到与AB都在EF的右侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠DCF=360°-3t-60°=300°-3t,∠BAC=110°-t,
要使AB∥CD,则∠DCF=∠BAC,
即300°-3t=110°-t,
解得t=95°,
此时(360°-60°)÷3=100,
∴40<t<100;
③CD旋转到与AB都在EF的左侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠DCF=3t-(180°-60°+180°)=3t-300°,∠BAC=t-110°,
要使AB∥CD,则∠DCF=∠BAC,
即3t-300°=t-110°,
解得t=95°,
此时t>110,
∵95<110,
∴此情况不存在.
综上所述,t为5秒或95秒时,CD与AB平行.
点评:本题考查了平行线的判定,读懂题意并熟练掌握平行线的判定方法是解题的关键,要注意分情况讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
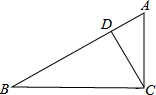 如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )
如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在四边形ABCD中,AB⊥BC,AD⊥DC,连接BD,AC,且DE⊥AC于E,交AB于F,求证:△AFD∽△ADB.
如图,在四边形ABCD中,AB⊥BC,AD⊥DC,连接BD,AC,且DE⊥AC于E,交AB于F,求证:△AFD∽△ADB. 如图,两个同心圆被两条半径截得
如图,两个同心圆被两条半径截得
 如图,∠AOB=70°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
如图,∠AOB=70°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数. 如图,∠B=40°,∠C=20°,∠CDB=3∠A,求∠A的度数.
如图,∠B=40°,∠C=20°,∠CDB=3∠A,求∠A的度数. 如图所示,九年级某兴趣小组要测量校园内的教学楼AB的高度,在地面上C点用测角仪测得楼顶A点的仰角∠AFE=60°,再沿着直线BC后退8m到达点D,在D点又测得楼顶A的仰角∠AGE=45°,已知测角仪的高度CF为1.6m.求教学楼AB的高度.(结果保留小数点后一位,
如图所示,九年级某兴趣小组要测量校园内的教学楼AB的高度,在地面上C点用测角仪测得楼顶A点的仰角∠AFE=60°,再沿着直线BC后退8m到达点D,在D点又测得楼顶A的仰角∠AGE=45°,已知测角仪的高度CF为1.6m.求教学楼AB的高度.(结果保留小数点后一位, 如图,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F,若CF⊥AD,AB=2,求DE的长.
如图,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F,若CF⊥AD,AB=2,求DE的长.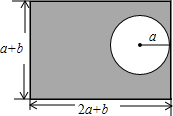 某个居民小区的长方形花园的长、宽分别为2a+b和a+b,中间有一个半径为a的圆形游乐场(如图),请你用代数式表示图中阴影部分的面积,再求当a=5米,b=10米时阴影部分面积(π取3.14).
某个居民小区的长方形花园的长、宽分别为2a+b和a+b,中间有一个半径为a的圆形游乐场(如图),请你用代数式表示图中阴影部分的面积,再求当a=5米,b=10米时阴影部分面积(π取3.14).