题目内容
15. 如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )
如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )| A. | 30° | B. | 25° | C. | 40° | D. | 20° |
分析 连结OC,如图,先根据切线的性质得∠OCD=90°,再利用直角三角形斜边上的中线性质得BC=BO=BD,则可判断△OBC为等边三角形,所以∠BOC=60°,然后根据等腰三角形的性质和三角形外角性质求∠A的度数.
解答 解:连结OC,如图,
∵CD相切圆O于点C,
∴OC⊥CD,
∴∠OCD=90°,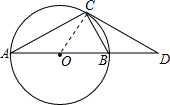
∵OB=BD,
∴BC=BO=BD,
∴OC=OB=BC,
∴△OBC为等边三角形,
∴∠BOC=60°,
而OA=OC,
∴∠A=∠OCA,
而∠BOC=∠A+∠OCA,
∴∠A=$\frac{1}{2}$∠BOC=30°.
故选A.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
3. 如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )
如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )
 如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )
如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )| A. | A$\sqrt{6}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{2}$ | D. | 3 |
7.抛物线y=-(x+2)2-5的顶点坐标是( )
| A. | (-2,5) | B. | (2,5) | C. | (-2,-5) | D. | (2,-5) |
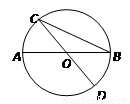
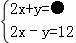 的解为
的解为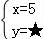 ,由于不小心,滴上了两滴墨水,刚好遮住了两个数●和★,请你帮他找回●这个数,●=______.
,由于不小心,滴上了两滴墨水,刚好遮住了两个数●和★,请你帮他找回●这个数,●=______.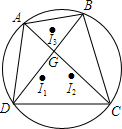 如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.
如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.
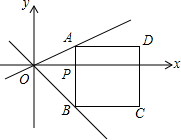 如图,直角坐标系中,点P(t,0)是x轴上的一个动点,过点P作y轴的平行线,分别与直线y=$\frac{1}{2}$x,直线y=-x交于A,B两点,以AB为边向右侧作正方形ABCD.
如图,直角坐标系中,点P(t,0)是x轴上的一个动点,过点P作y轴的平行线,分别与直线y=$\frac{1}{2}$x,直线y=-x交于A,B两点,以AB为边向右侧作正方形ABCD. 如图,P是∠BAC的平分线上一点,PD⊥AC,垂足为D.AB与以P为圆心、PD为半径的圆相切吗?请说明理由.
如图,P是∠BAC的平分线上一点,PD⊥AC,垂足为D.AB与以P为圆心、PD为半径的圆相切吗?请说明理由.