题目内容
3. 如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )
如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )| A. | A$\sqrt{6}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{2}$ | D. | 3 |
分析 连接OP,OQ,由PQ为圆O的切线,利用切线的性质得到OQ与PQ垂直,利用勾股定理列出关系式,由OP最小时,PQ最短,根据垂线段最短得到OP垂直于AB时最短,利用面积法求出此时OP的值,再利用勾股定理即可求出PQ的最短值.
解答 解:连接OP、OQ,如图所示,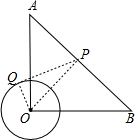
∵PQ是⊙O的切线,
∴OQ⊥PQ,
根据勾股定理知:PQ2=OP2-OQ2,
∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=4$\sqrt{2}$,
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•OP,即OP=$\frac{OA•OB}{AB}$=2$\sqrt{2}$,
∴PQ=$\sqrt{O{P}^{2}-O{Q}^{2}}$=$\sqrt{(2\sqrt{2})^{2}-{1}^{2}}$=$\sqrt{7}$,
故选B.
点评 此题考查了切线的性质,勾股定理的应用,熟练掌握切线的性质是解本题的关键,注意:圆的切线垂直于过切点的半径.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15. 如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )
如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )
 如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )
如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )| A. | 30° | B. | 25° | C. | 40° | D. | 20° |
12. 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.
(1)求出该函数与x轴的交点坐标、与y轴的交点坐标;
(2)在平面直角坐标系中,用描点法画出该二次函数的图象;
(3)根据图象回答:
①当自变量x的取值范围满足什么条件时,y<0?
②当0≤x<3时,y的取值范围是多少?
 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.(1)求出该函数与x轴的交点坐标、与y轴的交点坐标;
(2)在平面直角坐标系中,用描点法画出该二次函数的图象;
| x | … | … | |||||
| y | … | … |
①当自变量x的取值范围满足什么条件时,y<0?
②当0≤x<3时,y的取值范围是多少?
 (k≠0)满足:当x<0时,y随x的增大而减小.若该反比例函数的图象与直线y=﹣x+
(k≠0)满足:当x<0时,y随x的增大而减小.若该反比例函数的图象与直线y=﹣x+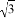 k都经过点P,且|OP|=
k都经过点P,且|OP|=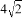 ,则实数k的值为__.
,则实数k的值为__.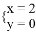 B.
B. 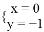 C.
C. 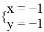 D.
D. 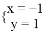
 如图所示,过⊙0上一点A作弦AB和直线MN,过点O作OB垂线交AB于点P,交MN点C,若CP=CA,试说明MN是⊙0的切线.
如图所示,过⊙0上一点A作弦AB和直线MN,过点O作OB垂线交AB于点P,交MN点C,若CP=CA,试说明MN是⊙0的切线.