题目内容
7.抛物线y=-(x+2)2-5的顶点坐标是( )| A. | (-2,5) | B. | (2,5) | C. | (-2,-5) | D. | (2,-5) |
分析 根据抛物线的顶点式求得顶点坐标即可判断.
解答 解:由y=-(x+2)2-5可知抛物线的顶点是(-2,-5),
故选C.
点评 本题考查了二次函数的性质,根据顶点式求得顶点坐标是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15. 如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )
如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )
 如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )
如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )| A. | 30° | B. | 25° | C. | 40° | D. | 20° |
12. 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.
(1)求出该函数与x轴的交点坐标、与y轴的交点坐标;
(2)在平面直角坐标系中,用描点法画出该二次函数的图象;
(3)根据图象回答:
①当自变量x的取值范围满足什么条件时,y<0?
②当0≤x<3时,y的取值范围是多少?
 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.(1)求出该函数与x轴的交点坐标、与y轴的交点坐标;
(2)在平面直角坐标系中,用描点法画出该二次函数的图象;
| x | … | … | |||||
| y | … | … |
①当自变量x的取值范围满足什么条件时,y<0?
②当0≤x<3时,y的取值范围是多少?
19.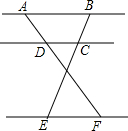 如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
 如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )| A. | $\frac{AD}{DF}$=$\frac{BC}{CE}$ | B. | $\frac{BC}{CE}$=$\frac{DF}{AD}$ | C. | $\frac{CD}{EF}$=$\frac{BC}{BE}$ | D. | $\frac{CD}{EF}$=$\frac{AD}{AF}$ |
16.已知点(-2,y1),(3,y2)都在直线y=-x+b上,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 无法确定 |
 和
和  ,乙口袋中装有两个相同的小球,它们的标号分别为
,乙口袋中装有两个相同的小球,它们的标号分别为  和
和  ,丙口袋中装有三个相同的小球,它们的标号分别为
,丙口袋中装有三个相同的小球,它们的标号分别为  ,
, ,
, .从这
.从这  个口袋中各随机取出一个小球.
个口袋中各随机取出一个小球. B.
B. 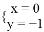 C.
C. 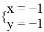 D.
D. 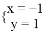
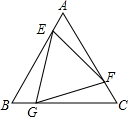 等边△ABC的面积为1,E、F、G是其各条边上的5等分点,其位置如图,那么三角形EFG的面积为$\frac{13}{25}$.
等边△ABC的面积为1,E、F、G是其各条边上的5等分点,其位置如图,那么三角形EFG的面积为$\frac{13}{25}$.