题目内容
10.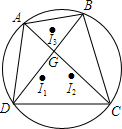 如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.
如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.
分析 分别连接AI3,AI1,DI1,DI2,CI1,CI2,延长I3G交I1I2于点H,根据I1、I2、I3分别为△ADC、△BDC、△ABG的内心得到∠AI3G=90°+$\frac{1}{2}$∠ABD,∠AI1C=90°+$\frac{1}{2}$∠ADC,从而得到点D、I1、I2、C四点共圆,利用∠I3HI1=360°-(∠1+∠2+∠AI3G+∠AI1H)=90°,得到I3G⊥I1I2.
解答 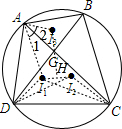 证明:分别连接AI3,AI1,DI1,DI2,CI1,CI2,
证明:分别连接AI3,AI1,DI1,DI2,CI1,CI2,
延长I3G交I1I2于点H,
∵I1、I2、I3分别为△ADC、△BDC、△ABG的内心,
∴∠AI3G=90°+$\frac{1}{2}$∠ABD,∠AI1C=90°+$\frac{1}{2}$∠ADC,
∴∠DI1C=90°+$\frac{1}{2}$∠DAC,∴∠DI2C=90°+$\frac{1}{2}$∠DBC,
∠1+∠2=$\frac{1}{2}$(∠DAC+∠BAC),
又∵∠DAC=∠DBC,
∴∠DI1C=∠DI2C,
∴点D、I1、I2、C四点共圆,
∴∠I2I1C=∠I2DC=$\frac{1}{2}$∠BDC=$\frac{1}{2}$∠BAC,
∴∠I3HI1=360°-(∠1+∠2+∠AI3G+∠AI1H)
∵∠1+∠2+∠AI3G+∠AI1H=$\frac{1}{2}$(∠DAC+∠BAC)+90°+$\frac{1}{2}$∠ABD+90°+$\frac{1}{2}$∠ADC-I2I1C
=180°+$\frac{1}{2}$(∠DAC+∠BAC+∠ABD+∠ADC+∠BAC)
=180°+$\frac{1}{2}$(∠ABD+∠DBC+∠ADC)
=270°,
∴∠I3HI1=360°-270°=90°,
∴I3G⊥I1I2.
点评 本题考查了三角形的五心的知识,解题的关键是正确的构造辅助线,利用院内接四边形的性质求解,属于难题,了解三角形的五心的性质是解决本题的重中之重.

 如图所示,A、B、C为长方体的三个顶点,则△ABC的形状是( )
如图所示,A、B、C为长方体的三个顶点,则△ABC的形状是( )| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
 如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )
如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )| A. | 30° | B. | 25° | C. | 40° | D. | 20° |
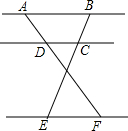 如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )| A. | $\frac{AD}{DF}$=$\frac{BC}{CE}$ | B. | $\frac{BC}{CE}$=$\frac{DF}{AD}$ | C. | $\frac{CD}{EF}$=$\frac{BC}{BE}$ | D. | $\frac{CD}{EF}$=$\frac{AD}{AF}$ |
| 小麦 | 玉米 | 黄豆 | |
| 亩产量(千克) | 600 | 900 | 330 |
| 销售单价(元/千克) | 2 | 1 | 2.5 |
(2)在保证小麦种植面积的情况下,玉米、黄豆同时均按整亩数套种,有几种“三种三收”套种方案?
(3)在(2)中的种植方案中,采用哪种套种方案才能使总销售价最高?最高价是多少?
 中,自变量
中,自变量 的取值范围是___ ;
的取值范围是___ ; ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.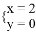 B.
B. 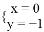 C.
C. 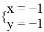 D.
D. 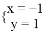
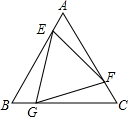 等边△ABC的面积为1,E、F、G是其各条边上的5等分点,其位置如图,那么三角形EFG的面积为$\frac{13}{25}$.
等边△ABC的面积为1,E、F、G是其各条边上的5等分点,其位置如图,那么三角形EFG的面积为$\frac{13}{25}$.