题目内容
20.如图,AB是公园的一圆形桌面的主视图,MN表示该桌面在路灯下的影子;CD则表示一个圆形的凳子.(1)请你在答题卡中标出路灯O的位置,并画出CD的影子PQ(要求保留画图痕迹,光线用虚线表示);
(2)若桌面直径和桌面与地面的距离均为1.2m,测得影子的最大跨度MN为2m,求路灯O与地面的距离.
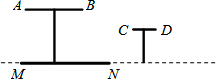
分析 (1)延长MA、NB,它们的交点即为路灯O的位置,然后再连结OC、OD,并延长交地面与P、Q点,则PQ为CD的影子;
(2)作OF⊥MN交AB于E,如图,AB=1.2m,EF=1.2m,MN=2m,证明△OAB∽△OMN,利用相似比计算出OF即可得到路灯O与地面的距离.
解答 解:(1)如图,点O和PQ为所作;
(2)作OF⊥MN交AB于E,如图,AB=1.2m,EF=1.2m,MN=2m,
∵AB∥MN,
∴△OAB∽△OMN,
∴AB:MN=OE:OF,即1.2:2=(OF-1.2):OF,解得OF=3(m).
答:路灯O与地面的距离为3m.
点评 本题考查了中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.如物体在灯光的照射下形成的影子就是中心投影.中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
15. 如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )
如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )
 如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )
如图,已知CD相切圆O于点C,BD=OB,则∠A的度数是( )| A. | 30° | B. | 25° | C. | 40° | D. | 20° |
12. 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.
(1)求出该函数与x轴的交点坐标、与y轴的交点坐标;
(2)在平面直角坐标系中,用描点法画出该二次函数的图象;
(3)根据图象回答:
①当自变量x的取值范围满足什么条件时,y<0?
②当0≤x<3时,y的取值范围是多少?
 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.(1)求出该函数与x轴的交点坐标、与y轴的交点坐标;
(2)在平面直角坐标系中,用描点法画出该二次函数的图象;
| x | … | … | |||||
| y | … | … |
①当自变量x的取值范围满足什么条件时,y<0?
②当0≤x<3时,y的取值范围是多少?
 B.
B.  C.
C.  D.
D. 
 如图所示,过⊙0上一点A作弦AB和直线MN,过点O作OB垂线交AB于点P,交MN点C,若CP=CA,试说明MN是⊙0的切线.
如图所示,过⊙0上一点A作弦AB和直线MN,过点O作OB垂线交AB于点P,交MN点C,若CP=CA,试说明MN是⊙0的切线.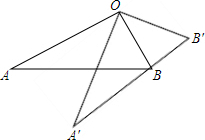 如图,∠AOB=90°,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanB=2,OB=5,则BB′=2$\sqrt{5}$.
如图,∠AOB=90°,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanB=2,OB=5,则BB′=2$\sqrt{5}$. 如图所示的图形绕虚线旋转一周得到的几何体的名称是圆锥.
如图所示的图形绕虚线旋转一周得到的几何体的名称是圆锥.