题目内容
3. 一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),如图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,则t的值为3.5.
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),如图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,则t的值为3.5.
分析 设线段AB所在直线的函数关系式为y=kx+b,待定系数法求出AB所在直线解析式,当x=0时,即为甲、乙两地距离,求出y=280,设快车的速度为每小时m千米,慢车的速度为每小时n千米,利用两车行驶距离得出等式方程求出即可.
解答 解:设线段AB所在直线的函数关系式为y=kx+b,
把(1.5,70)、(2,0)代入得;
$\left\{\begin{array}{l}{1.5k+b=70}\\{2k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-140}\\{b=280}\end{array}\right.$,
∴y=-140x+280
∴x=0时,y=280,即甲、乙两地间的距离为280千米,
设快车的速度为每小时m千米,慢车的速度为每小时n千米,
由题意得,$\left\{\begin{array}{l}{2m+2n=280}\\{2m-2n=40}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=80}\\{n=60}\end{array}\right.$,
∴t=$\frac{280}{80}$=3.5,
故答案为:3.5.
点评 此题主要考查了一次函数的应用以及二元一次方程组的应用,根据已知利用图象得出正确信息是解题关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
18.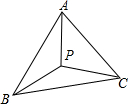 如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
 如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )| A. | 110° | B. | 130° | C. | 120° | D. | 140° |
15. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,且AD⊥BC,则∠B的度数为( )
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,且AD⊥BC,则∠B的度数为( )
 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,且AD⊥BC,则∠B的度数为( )
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,且AD⊥BC,则∠B的度数为( )| A. | 15° | B. | 25° | C. | 35° | D. | 45° |

 如图,△ABC中(AB>BC),AB=2AC,AC边上中线BD把△ABC的周长分成30和20两部分,求AB和BC的长.
如图,△ABC中(AB>BC),AB=2AC,AC边上中线BD把△ABC的周长分成30和20两部分,求AB和BC的长. 如图,在△ABC中,AC=BC,以BC为直径的半圆O交AC于D,交AB于E,连接BD,CE交于点F,经过点E作EG⊥BC于G,交BD于H,过点E作EM⊥AC于M.下列结论:
如图,在△ABC中,AC=BC,以BC为直径的半圆O交AC于D,交AB于E,连接BD,CE交于点F,经过点E作EG⊥BC于G,交BD于H,过点E作EM⊥AC于M.下列结论: 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于E,若PE=1.8cm,则AD与BC之间的距离为3.6cm.
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于E,若PE=1.8cm,则AD与BC之间的距离为3.6cm.