题目内容
14.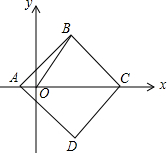 如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )
如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 过B点作BE⊥AC,垂足为E,根据正方形的性质可以得出E是AC的中点,根据A(-1,0),C(7,0)求出AC和BE的长度进而求出B点的坐标,再求出OB的长度,在Rt△OEB中,求出∠BOC的正弦值.
解答 解:过B点作BE⊥AC,垂足为E,
∵四边形ABCD是正方形,
∴E是AC中点,
∵A(-1,0),C(7,0),
∴AC=8,
∴BE=AE=4,
∴B点的坐标为(3,4),
∴OB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
在Rt△OEB中,
sin∠BOC=$\frac{BE}{OB}$=$\frac{4}{5}$,
故选A.
点评 本题主要考查正方形的性质的知识点,解答本题的关键是正确的作出辅助线,此题的难度一般,是一道非常不错的习题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

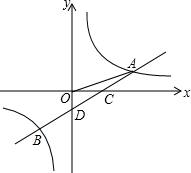 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知A(3,1),点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知A(3,1),点B的坐标为(m,-2). 如图,在△ABC中,D,E两点分别在边AB,AC上,AB=8cm,AC=6cm,AD=3cm,要使△ADE与△ABC相似,则线段AE的长为4或$\frac{9}{4}$cm.
如图,在△ABC中,D,E两点分别在边AB,AC上,AB=8cm,AC=6cm,AD=3cm,要使△ADE与△ABC相似,则线段AE的长为4或$\frac{9}{4}$cm.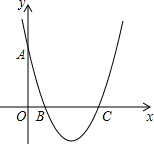 如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于B,C两点,其中B点坐标为(1,0),与y轴交于点A,A点坐标为(0,3)
如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于B,C两点,其中B点坐标为(1,0),与y轴交于点A,A点坐标为(0,3) 如图,点P是反比例函数在第二象限上的一点,且矩形PEOF的面积为5,则反比例函数的表达式为y=-$\frac{5}{x}$.
如图,点P是反比例函数在第二象限上的一点,且矩形PEOF的面积为5,则反比例函数的表达式为y=-$\frac{5}{x}$.