题目内容
11.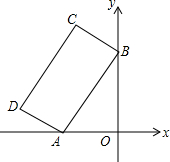 如图,矩形ABCD的两个顶点A,B在坐标轴上,AD:AB=1:2,且A(-2,0),∠BAO=60°,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过该矩形的顶点,则k=-2-$\sqrt{3}$或-6-$\sqrt{3}$.
如图,矩形ABCD的两个顶点A,B在坐标轴上,AD:AB=1:2,且A(-2,0),∠BAO=60°,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过该矩形的顶点,则k=-2-$\sqrt{3}$或-6-$\sqrt{3}$.
分析 过点D作DE⊥x轴于点E,过点C作CF⊥y轴于点F,再由A(-2,0),∠BAO=60°可知∠ABO=30°,故可得出AB的长,再由AD:AB=1:2求出AD的长,根据直角三角形的性质求出AE及DE的长可得出D点坐标,同理可得出C点坐标,再分函数的图象过C点与过D点两种情况讨论即可.
解答  解:过点D作DE⊥x轴于点E,过点C作CF⊥y轴于点F,
解:过点D作DE⊥x轴于点E,过点C作CF⊥y轴于点F,
∵A(-2,0),∠BAO=60°,
∴OA=2,∠ABO=30°,
∴AB=2OA=4,OB=AB•cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$.
∵AD:AB=1:2,
∴AD=2.
∵∠DAE+∠BAO=90°,
∴∠DAE=30°,
∴DE=$\frac{1}{2}$AD=1,AE=AD•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∴D(-2-$\sqrt{3}$,1);
在Rt△BCF中,
∵∠CBF+∠ABO=90°,
∴∠CBF=60°,
∴BF=BC•cos60°=2×$\frac{1}{2}$=1,CF=BC•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴C(-$\sqrt{3}$,1+2$\sqrt{3}$),
∴当反比例函数经过C点时,k=-$\sqrt{3}$×(1+2$\sqrt{3}$)=-6-$\sqrt{3}$;当反比例函数经过D点时,k=-2-$\sqrt{3}$.
故答案为:-2-$\sqrt{3}$或-6-$\sqrt{3}$.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
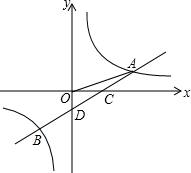 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知A(3,1),点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知A(3,1),点B的坐标为(m,-2).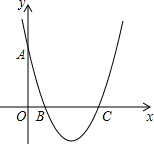 如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于B,C两点,其中B点坐标为(1,0),与y轴交于点A,A点坐标为(0,3)
如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于B,C两点,其中B点坐标为(1,0),与y轴交于点A,A点坐标为(0,3)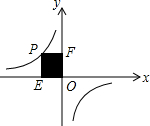 如图,点P是反比例函数在第二象限上的一点,且矩形PEOF的面积为5,则反比例函数的表达式为y=-$\frac{5}{x}$.
如图,点P是反比例函数在第二象限上的一点,且矩形PEOF的面积为5,则反比例函数的表达式为y=-$\frac{5}{x}$. 如图,在矩形ABCD中,BC=2,M为对角线BD的中点,连接CM,以CM为直径作⊙O交BD于点E,连接AE,当直线AE与⊙O相切时,AB的长为$\sqrt{6}$-$\sqrt{2}$.
如图,在矩形ABCD中,BC=2,M为对角线BD的中点,连接CM,以CM为直径作⊙O交BD于点E,连接AE,当直线AE与⊙O相切时,AB的长为$\sqrt{6}$-$\sqrt{2}$.