Question

14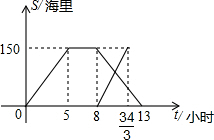．钓鱼岛是我国渤海海峡上的一颗明珠，渔产丰富．一天某渔船离开港口前往钓鱼岛A海域捕鱼．捕捞一段时间后，发现一外国舰艇进入我国水域向钓鱼岛驶来，渔船向渔政部门报告，并立即返航，渔政船接到报告后，立即从该港口出发赶往钓鱼岛．如图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象．（假设渔船与渔政船沿同一航线航行）
（1）直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式．
（2）求渔船和渔政船相遇时，两船与钓鱼岛A海域的距离．
（3）在渔政船驶往钓鱼岛的过程中，求渔船从港口出发经过多长时间与渔政船相距30海里？

Answer 1

分析 （1）根据函数图象利用待定系数法求得函数的解析式；
（2）求得渔政船距黄岩岛的距离时间的函数关系式，求两个函数解析式组成的方程组即可；
（3）根据渔船与渔政船相距30海里即可列方程求解．

解答 解：（1）当0≤t≤5时，s=30，
当5＜t≤8时，s=150，
设渔船返航时离开港口的距离s和时间t之间的函数关系式是：s=kx+b，
根据题意得：$\left\{\begin{array}{l}{8k+b=150}\\{13k+b=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-30}\\{b=390}\end{array}\right.$．
则函数解析式是s=-30t+390（8≤t≤13）；
（2）设渔政船的函数解析式是s=mt+n，则$\left\{\begin{array}{l}{8m+n=0}\\{\frac{34}{3}m+n=150}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{m=45}\\{n=-360}\end{array}\right.$，
则函数的解析式是s=45t-360，
根据题意得：$\left\{\begin{array}{l}{s=-30t+390}\\{s=45t-360}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{t=10}\\{s=90}\end{array}\right.$．
两船与钓鱼岛A海域的距离是150-90=60海里；
（3）当（-30t+390）-（45t-360）=30时，解得：t=$\frac{48}{5}$，
当（45t-360）-（-30t+390）=30时，解得：t=$\frac{52}{5}$．
则当$\frac{48}{5}$或$\frac{52}{5}$小时时，两船相距30海里．

点评 本题考查了一次函数的应用，解答一次函数的应用问题中，要注意自变量的取值范围还必须使实际问题有意义．