题目内容
19．若（x+2）（x-n）=x2+mx-12，则m-n=-10．分析 先将左边展开，再根据等式的性质，得到关于m和n的方程组，求得m和n的值即可．
解答 解：∵（x+2）（x-n）=x2+mx-12，
∴x2-nx+2x-2n=x2+mx-12，
即x2+（2-n）x-2n=x2+mx-12，
∴$\left\{\begin{array}{l}{2-n=m}\\{-2n=-12}\end{array}\right.$
解得$\left\{\begin{array}{l}{m=-4}\\{n=6}\end{array}\right.$
∴m-n=-4-6=-10
故答案为：-10
点评 本题主要考查了整式的乘法，解决问题的关键是掌握多项式乘多项式的法则：多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．下列各式中不是分式的是（ ）
| A． | $-\frac{1}{2a\;}$ | B． | $\frac{x}{\;x+y}$ | C． | $\frac{2}{2\;+y}$ | D． | $\frac{2+x}{3}$ |
7．数a的相反数是（ ）
| A． | |a| | B． | $\frac{1}{a}$ | C． | -a | D． | $\sqrt{a}$ |
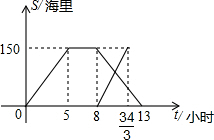钓鱼岛是我国渤海海峡上的一颗明珠，渔产丰富．一天某渔船离开港口前往钓鱼岛A海域捕鱼．捕捞一段时间后，发现一外国舰艇进入我国水域向钓鱼岛驶来，渔船向渔政部门报告，并立即返航，渔政船接到报告后，立即从该港口出发赶往钓鱼岛．如图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象．（假设渔船与渔政船沿同一航线航行）
某学校为了推动运动普及，拟成立多个球类运动社团，为此，学生会采取抽样调查的方法，从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好（要求每位同学只能选择其中一种自己喜欢的球类运动），并将调查结果绘制成了如下条形统计图和扇形统计图（不完整）．请你根据图中提供的信息，解答下列问题：