题目内容
19.已知不等式ax2+bx+c<0(a≠0)的解是x<2,或x>3,求不等式bx2+ax+c>0的解.分析 由不等式ax2+bx+c<0(a≠0)的解集为x<2或x>3,可得2,3为方程ax2+bx+c=0的两根,利用根与系数的关系得到系数的比,变形后得到b=-5a,c=6a.由此求出方程bx2+ax+c的两根,则不等式bx2+ax+c>0的解集可求.
解答 解:∵不等式ax2+bx+c<0(a≠0)的解是x<2,或x>3,
∴2,3为方程ax2+bx+c=0的两个实数根,且a<0.
∴$\left\{\begin{array}{l}{-\frac{b}{a}=2+3}\\{\frac{c}{a}=2×3}\end{array}\right.$,
则b=-5a,c=6a.
代入不等式bx2+ax+c>0可得-5ax2+ax+6a>0,
∵a<0.
∴-5x2+x+6<0,即-(x+1)(5x-6)<0,
解得x<-1或x>$\frac{6}{5}$,
即不等式bx2+ax+c>0的解集是x<-1或x>$\frac{6}{5}$.
点评 本题考查了一元二次不等式的解法、一元二次方程的根与系数的关系,考查了推理能力和计算能力,属于基础题.

练习册系列答案
相关题目
7.在三角形的角平分线、中线、高线中,属于直线的有(每种线只有一条)( )
| A. | 0条 | B. | 1条 | C. | 2条 | D. | 3条 |
4.已知关于x不等式2x2+bx-c>0的解集为{x|x<-1或x>3},则关于x的不等式bx2+cx+4≥0的解集为( )
| A. | {x|x≤-2或x≥$\frac{1}{2}$} | B. | {x|x≤-$\frac{1}{2}$或x≥2} | C. | {x|-$\frac{1}{2}$≤x≤2} | D. | {x|-2≤x≤$\frac{1}{2}$} |
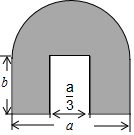 如图是一个工件的横断面及其尺寸.(单位:cm).
如图是一个工件的横断面及其尺寸.(单位:cm). 如图,点C、E和点B、D、F分别在∠GAH的两边上,且∠A=18°,AB=BC=CD=DE=EF,则∠GEF=90度.
如图,点C、E和点B、D、F分别在∠GAH的两边上,且∠A=18°,AB=BC=CD=DE=EF,则∠GEF=90度.