题目内容
14.在△ABC中,∠C=90°,3a=$\sqrt{3}$b,c=10,∠A=30°,a=5,b=5$\sqrt{3}$.分析 根据在△ABC中,∠C=90°,3a=$\sqrt{3}$b,c=10,可以求得∠A的正切值,从而可以求得∠A的度数,进而求得a、b的值.
解答 解:∵在△ABC中,∠C=90°,3a=$\sqrt{3}$b,c=10,
∴$\frac{a}{b}=\frac{\sqrt{3}}{3}$,
即tanA=$\frac{\sqrt{3}}{3}$,
∴∠A=30°,
∴a=5,b=5$\sqrt{3}$,
故答案为:30°,5,5$\sqrt{3}$
点评 本题考查解直角三角形,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
6.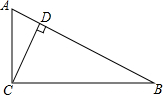 如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,其中斜边上的高为( )
如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,其中斜边上的高为( )
 如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,其中斜边上的高为( )
如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,其中斜边上的高为( )| A. | 6cm | B. | 8.5cm | C. | $\frac{60}{13}$cm | D. | $\frac{30}{13}$cm |
3.下列算式中,错误的是( )
| A. | a(a+b)+b(a+b)=a2+2ab+b2 | B. | x(x-y)+y(x-y)=x2-y2 | ||
| C. | a(a2-ab+b2)+b(a2-ab+b2)=a3+b3 | D. | x(x-y)-y(x-y)=y2-x2 |