题目内容
13.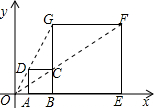 如图所示,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A,B,E在x轴上.
如图所示,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A,B,E在x轴上.(1)若点F的坐标为(4.5,3),直接写出点C和点A的坐标;
(2)若正方形BEFG的边长为6,求点C的坐标.
分析 (1)利用关于原点为位似中心的对应点的坐标特征,把F点的横纵坐标都乘以$\frac{1}{3}$即可得到C点坐标,然后利用正方形的性质写出A点坐标;
(2)先利用位似的性质得到正方形ABCD的边长为2,再利用相似比求出OB,从而可得到C点坐标.
解答 解:(1)C点坐标为($\frac{3}{2}$,1),A点坐标为($\frac{1}{2}$,0);
(2)∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,
∴正方形BEFG的边长为6,则正方形ABCD的边长为2,OB:OE=1:3,
∴OB:(OB+6)=1:3,解得OB=3,
∴点C的坐标为(3,2).
点评 本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.

练习册系列答案
相关题目
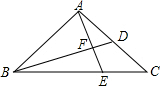 如图,在△ABC中,BD是AC边上的中线,E是BC上一点,AE与BD相交于点F.
如图,在△ABC中,BD是AC边上的中线,E是BC上一点,AE与BD相交于点F.
 如图,在矩形ABCD中,AB=15,BC=8,E是AB上一点,沿DE折叠使A落在DB上,求AE的长.
如图,在矩形ABCD中,AB=15,BC=8,E是AB上一点,沿DE折叠使A落在DB上,求AE的长.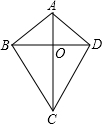 如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的个数有( )
如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的个数有( )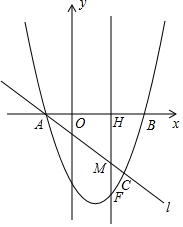 如图,抛物线y=x2+bx+c与x轴交A(-1,0)B(3,0)两点,直线l与抛物线交于A,C两点,其中C点的横坐标为2.
如图,抛物线y=x2+bx+c与x轴交A(-1,0)B(3,0)两点,直线l与抛物线交于A,C两点,其中C点的横坐标为2.