题目内容
3．
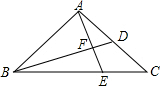如图，在△ABC中，BD是AC边上的中线，E是BC上一点，AE与BD相交于点F．求证：$\frac{BE}{BC}$=$\frac{EF}{AF}$．
分析 作EH∥AC交BD于H，根据平行线分线段成比例定理得到 $\frac{EH}{AD}$=$\frac{EF}{AF}$，$\frac{BE}{BC}$=$\frac{EH}{CD}$，由AD=CD，即可证明$\frac{EF}{AF}$=$\frac{BE}{BC}$．
解答 证明：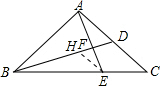
作EH∥AC交BD于H，
∴$\frac{EH}{AD}$=$\frac{EF}{AF}$，$\frac{BE}{BC}$=$\frac{EH}{CD}$，
∵AD=CD，
∴$\frac{EF}{AF}$=$\frac{BE}{BC}$．
点评 本题考查的是平行线分线段成比例定理的应用，正确作出辅助线、灵活运用定理、找准对应关系是解题的关键．
练习册系列答案
相关题目
11．点P（-3，5）关于y轴的对称点P'的坐标是（ ）
| A． | （3，5） | B． | （5，-3） | C． | （3，-5） | D． | （-3，-5） |
18．
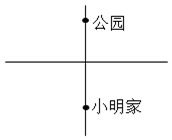如图，小明周末到公园走到十字路口处，记不清前面哪条路通往公园，那么他能一次选对路的概率是（ ）
如图，小明周末到公园走到十字路口处，记不清前面哪条路通往公园，那么他能一次选对路的概率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | 0 |
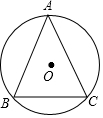已知⊙O的半径为2，△ABC内接于⊙O，$\widehat{AB}$、$\widehat{BC}$、$\widehat{AC}$的长之比为3：2：3，求BC的长．
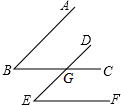已知：①如图，AB∥DE，BC∥EF，BC与DE相交于点G．请你猜想∠B与∠E之间具有什么数量关系，并说明理由．②请猜测：如果一个角的两条边与另一个角的两条边分别平行，那么这两个角的数量关系是相等或互补．
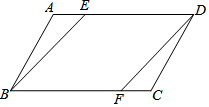如图，ABCD是平行四边形，E、F分别是AD、BC上一点，且AE=CF．求证：EBFD是平行四边形．
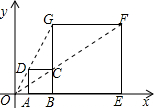如图所示，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为1：3，点A，B，E在x轴上．