题目内容
5.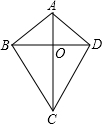 如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的个数有( )
如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据全等三角形的性质得出∠AOB=∠AOD=90°,OB=OD,AB=AD,再根据全等三角形的判定定理得出△ABC≌△ADC,进而得出其它结论.
解答 解:∵△ABO≌△ADO,
∴∠AOB=∠AOD=90°,OB=OD,AB=AD,
∴AC⊥BD,故①正确;
∵四边形ABCD的对角线AC、BD相交于点O,OB=OD,AC⊥BD,
∴BC=DC,②正确;
在△ABC和△ADC中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{BC=DC}&{\;}\\{AC=AC}&{\;}\end{array}\right.$,
∴△ABC≌△ADC(SSS),故③正确;
AB=AD,BC=DC,没有条件得出DA=DC,④不正确;
正确结论有3个,
故选:C.
点评 本题考查了全等三角形的判定和性质、等腰三角形的性质,掌握全等三角形的判定方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
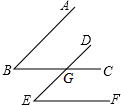 已知:①如图,AB∥DE,BC∥EF,BC与DE相交于点G.请你猜想∠B与∠E之间具有什么数量关系,并说明理由.②请猜测:如果一个角的两条边与另一个角的两条边分别平行,那么这两个角的数量关系是相等或互补.
已知:①如图,AB∥DE,BC∥EF,BC与DE相交于点G.请你猜想∠B与∠E之间具有什么数量关系,并说明理由.②请猜测:如果一个角的两条边与另一个角的两条边分别平行,那么这两个角的数量关系是相等或互补. 如图,在△ABC中,AB=5,BC=3,CA=4,AD平分∠BAC,点M,N分别为AD,AC上的动点,则CM+MN的最小值是2.4.
如图,在△ABC中,AB=5,BC=3,CA=4,AD平分∠BAC,点M,N分别为AD,AC上的动点,则CM+MN的最小值是2.4.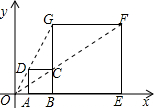 如图所示,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A,B,E在x轴上.
如图所示,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A,B,E在x轴上. 如图,在△ABC中,AB=AC,BD⊥AC于D,若∠ABC=72°,求∠ABD的度数.
如图,在△ABC中,AB=AC,BD⊥AC于D,若∠ABC=72°,求∠ABD的度数.