题目内容
11.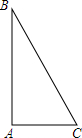 已知:如图,Rt△ABC中,∠BAC=90°.
已知:如图,Rt△ABC中,∠BAC=90°.(1)按要求作出图形:
①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE.
(2)猜想(1)中线段AD与BE的大小关系,并证明你的结论.
解:(1)完成作图
(2)AD与BE的大小关系是AD=BE.
分析 (1)根据已知条件画出图形即可;
(2)在AE上截取AF=AC,连结BF,根据全等三角形的判定定理求出△BAF≌△BAC,求出△BFE≌△DCA,即可得出答案.
解答 解:(1)如图: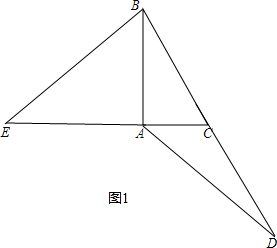 ;
;
(2)AD=BE,
理由是:在AE上截取AF=AC,连结BF,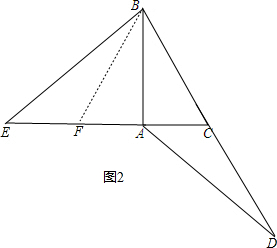
∵∠BAC=90°,
∴∠BAF=180°-90°=90°,
∴∠BAC=∠BAF,
在△ABF与△ABC中
$\left\{\begin{array}{l}AB=AB\\∠BAF=∠BAC\\ AF=AC\end{array}\right.$
∴△ABF≌△ABC(SAS),
∴BF=BC,AF=AC,∠BCA=∠BFA,
∵∠BFE+∠BFA=180°,∠BCA+∠DCA=180°,
∴∠BFE=∠DCA,
∵BC=DC,BC=BF,
∴BF=DC,
∵AC=AF,AE=2AC=AF+EF,
∴EF=AC=AF,
在△BFE和△DCA中
$\left\{\begin{array}{l}{BF=DC}\\{∠BFE=∠DCA}\\{FE=CA}\end{array}\right.$
∴△BFE≌△DCA,
∴AD=BE,
故答案为:AD=BE.
点评 本题考查了全等三角形的性质和判定的应用,能综合运用定理进行推理是解此题的关键,题目比较好,有一定的难度.

练习册系列答案
相关题目
 如图,点C在线段AB上,D是线段AC的中点,若BD=5cm,BC=2cm,则AB的长度为8cm.
如图,点C在线段AB上,D是线段AC的中点,若BD=5cm,BC=2cm,则AB的长度为8cm.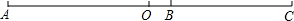 如图:AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长度.(括号内注理由)
如图:AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长度.(括号内注理由)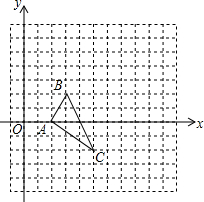 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,0),B(3,2),C(5,-2).以原点O为位似中心,在y轴的右侧将△ABC放大为原来的两倍得到△A′B′C′.
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,0),B(3,2),C(5,-2).以原点O为位似中心,在y轴的右侧将△ABC放大为原来的两倍得到△A′B′C′.