题目内容
2．
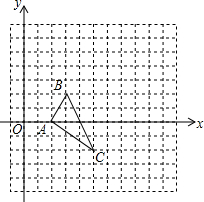如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（2，0），B（3，2），C（5，-2）．以原点O为位似中心，在y轴的右侧将△ABC放大为原来的两倍得到△A′B′C′．（1）画出△A′B′C′；
（2）分别写出B，C两点的对应点B′，C′的坐标．
分析 （1）由以原点O为位似中心，在y轴的右侧将△ABC放大为原来的两倍得到△A′B′C′，根据位似的性质，可求得点′、B′、C′的坐标，继而画出△A′B′C′；
（2）由（1）即可求得B，C两点的对应点B′，C′的坐标．
解答 解：（1）∵以原点O为位似中心，在y轴的右侧将△ABC放大为原来的两倍得到△A′B′C′，
∴A′（4，0），B′（6，4），C′（10，-4）；
如图画出△A′B′C′：
（2）由（1）得：B′（6，4），C′（10，-4）．
点评 此题考查了位似图形变换．注意掌握关于原点位似的图形的变化特点是关键．
练习册系列答案
相关题目
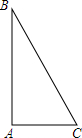已知：如图，Rt△ABC中，∠BAC=90°．
在△ABC中，D为AB边上一点，DE∥BC交AC于点E，若$\frac{AD}{DB}=\frac{3}{5}$，DE=6，则BC的长度为（ ）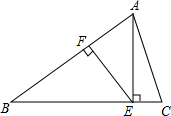
已知：如图，等腰△ABC中，AB=BC，AE⊥BC于E，EF⊥AB于F，若CE=2，cos∠AEF=$\frac{4}{5}$，求BE的长．
11．下列各式中是单项式的是（ ）
| A． | $\sqrt{7}$ | B． | $\sqrt{2a}$ | C． | $\frac{a-1}{2}$ | D． | $\frac{1}{a}$ |