题目内容
5.在一个不透明的袋子装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m(m>1)个红球,再先从袋子中随机摸出1个球,将“摸出黑球”记为事件A.请完成下面表格:
| 事件A | 必然事件 | 随机事件 |
| m的值 | 4 | 2或3 |
分析 (1)当袋子中全部为黑球时,摸出黑球才是必然事件,否则就是随机事件;
(2)利用概率公式计算即可.
解答 解:(1)当袋子中全为黑球,即摸出4个红球时,摸到黑球是必然事件;
当摸出2个或3个时,摸到黑球为随机事件,
故答案为:4;2或3;
(2)m=2时,P(摸出黑球)=$\frac{6}{8}$=$\frac{3}{4}$.
点评 本题考查的是概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
20.如图,四个全等的直角三角形纸片既可以拼成(内角不是直角)的菱形ABCD,也可以拼成正方形EFGH,则菱形ABCD面积和正方形EFGH面积之比为( )
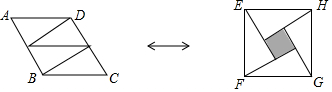

| A. | 1 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2}{3}$ |
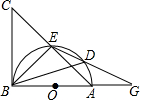 如图,AB是半⊙O的直径,点D是圆弧AE上一点,且∠BDE=∠CBE,点C在AE的延长线上
如图,AB是半⊙O的直径,点D是圆弧AE上一点,且∠BDE=∠CBE,点C在AE的延长线上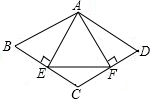 如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连结EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是①③④(只需填写正确结论的序号).
如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连结EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是①③④(只需填写正确结论的序号).
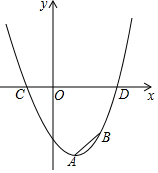 二次函数y=x2-2x-c 的图象如图所示,A,B两点的纵坐标分别为-4,-3,且AB=$\sqrt{2}$.
二次函数y=x2-2x-c 的图象如图所示,A,B两点的纵坐标分别为-4,-3,且AB=$\sqrt{2}$.