题目内容
18.有若干个数,第一个数记为a1,第二个数记为a2,…,第n个数记为an.若a1=$\frac{1}{2}$,从第2个数开始,每个数都等于“1减去该数前面那个数得到的差的倒数”.试计算:a2=2,a3=-1,a4=$\frac{1}{2}$,a5=2.这些数有什么规律吗?根据你发现的规律,请计算a2014是多少?分析 根据规定的运算方法,依次计算,由计算结果发现每3个数为一个循环组依次循环,用2014除以3,再根据商和余数的情况确定出答案.
解答 解:∵a1=$\frac{1}{2}$,
∴a2=$\frac{1}{1-\frac{1}{2}}$=2,
a3=$\frac{1}{1-2}$=-1,
a4=$\frac{1}{1-(-1)}$=$\frac{1}{2}$,
a5=$\frac{1}{1-\frac{1}{2}}$=2,
…
数列以$\frac{1}{2}$,2,-1三个数字依次不断循环出现,
∵2014÷3=671余1,
∴a2014是第672循环组的第一个数,与a1相同,
∴a2014=$\frac{1}{2}$.
故答案为:2,-1,$\frac{1}{2}$,2.
点评 此题考查数字的变化规律,理解规定的运算方法,计算得出每3个数为一个循环组依次循环是解题关键.

练习册系列答案
相关题目
10.某乡有四个村生产草莓,每千克售2.25元.填表:(用计算器计算)
| 村别 | 甲村 | 乙村 | 丙村 | 丁村 | 四村合计 |
| 数量(kg) | 12560 | 8974 | 9670 | 8796 | 40000 |
| 金额(元) | 28260 | 20191.5 | 21757.5 | 19791 | 90000 |
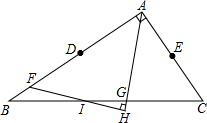 已知:△ABC中,D是AB的中点,E是AC的中点,F是DB上的一点,DF=AE,AG是∠BAC的角平分线,FH⊥AG垂足是H,FH、BC相交于I,求证:BI=CI.
已知:△ABC中,D是AB的中点,E是AC的中点,F是DB上的一点,DF=AE,AG是∠BAC的角平分线,FH⊥AG垂足是H,FH、BC相交于I,求证:BI=CI. 如图,在△ABC中,AB=AC,AD和BE是高,它们交于点H,且AE=BE.求证:
如图,在△ABC中,AB=AC,AD和BE是高,它们交于点H,且AE=BE.求证: 如图,A(3,0),B(0,3),C(1,4),求△ABC的面积.
如图,A(3,0),B(0,3),C(1,4),求△ABC的面积. 如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,求证:AO⊥BC.
如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,求证:AO⊥BC.