题目内容
13.已知△ABC的三边长为3、4、5,则它的外接圆的半径为2.5,内切圆的半径为1.分析 先证明△ABC为直角三角形,然后可知外接圆的半径为斜边的一半,然后
解答 解:如图所示:连接DF,EF.
∵32+42=52,
∴△ABC为直角三角形.
∴它的外接圆的半径为=$\frac{1}{2}×5=2.5$.
∵AB是圆的切线,DF是圆的半径,
∴DF⊥AB.
同理EF⊥BC.
∴∠FDB=∠DBE=∠BEF=90°.
∴四边形DBEF是矩形.
∵DF=EF,
∴四边形DBEF是正方形.
∴DB=BE.
设圆F的半径为r,则4-r+3-r=5.
解得:r=1.
∴它的内切圆的半径为1.
故答案为:2.5;1.
点评 本题主要考查的是三角形的内切圆、外接圆,利用切线长定理列出方程是解题的关键.

练习册系列答案
相关题目
1.为了解某校七年级300名学生的视力情况,从中抽出60名学生进行调查,以下说法正确的是( )
| A. | 该校七年级学生是总体 | B. | 该校七年级的每一个学生是个体 | ||
| C. | 抽出的60名学生是样本 | D. | 样本容量是60 |
3.关于x的方程$\frac{m}{x-1}$=1的解为正数,则m的取值范围是( )
| A. | m>-1 | B. | m≠0 | C. | m>1且m≠0 | D. | m>-1且m≠0 |
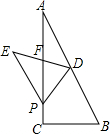 在Rt△ABC中,BC=4,AC=8,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.
在Rt△ABC中,BC=4,AC=8,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.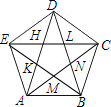 已知:如图,连结正五边形ABCDE各条对角线,就得到一个五角星图案,
已知:如图,连结正五边形ABCDE各条对角线,就得到一个五角星图案,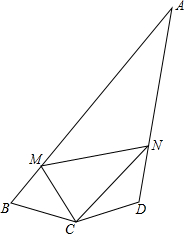 如图,四边形ABCD中,∠B+∠D=180°,∠BCD=150°,CB=CD,M,N为AB、AD上的两个动点,且∠MCN=75°.求证:MN=BM+DN.
如图,四边形ABCD中,∠B+∠D=180°,∠BCD=150°,CB=CD,M,N为AB、AD上的两个动点,且∠MCN=75°.求证:MN=BM+DN.