题目内容
9.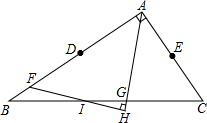 已知:△ABC中,D是AB的中点,E是AC的中点,F是DB上的一点,DF=AE,AG是∠BAC的角平分线,FH⊥AG垂足是H,FH、BC相交于I,求证:BI=CI.
已知:△ABC中,D是AB的中点,E是AC的中点,F是DB上的一点,DF=AE,AG是∠BAC的角平分线,FH⊥AG垂足是H,FH、BC相交于I,求证:BI=CI.
分析 延长FH交AC的延长线于点M,作CN∥AB,交FM于点N,易证△AFH≌△AFM,得到∠M=∠AFH,AF=AM,由CN∥AB,得到∠CNM=∠AFH,∠B=∠ICN,则∠CNM=∠M,所以CM=CN,根据CM=AD-EC,BF=AD-DF,DF=CE=AE,得到BF=CN=CM,可证明△BFI≌△CIN,则BI=CI.
解答 证明:延长FH交AC的延长线于点M,作CN∥AB,交FM于点N,
∵AG是∠BAC的角平分线,FH⊥AG,
∴∠FAH=∠MAH,∠AHF=∠AHM=90°,
在△AFH和△AFM中,
$\left\{\begin{array}{l}{∠FAH=∠MAH}\\{AH=AH}\\{∠AHF=∠AHM}\end{array}\right.$,
∴△AFH≌△AFM,
∴∠M=∠AFH,AF=AM,
∵CN∥AB,
∴∠CNM=∠AFH,∠B=∠ICN,
∴∠CNM=∠M,
∴CM=CN,
∵CM=AM-AC=AF-AC=AD+DF-AE-EC,DF=AE,
∴CM=AD-EC
∵BF=AB-AF=2AD-AD-DF=AD-DF,DF=CE,
∴BF=CN=CM,
在△BFI和△CIN中,
$\left\{\begin{array}{l}{∠B=∠ICN}\\{∠BIF=∠CIN}\\{BF=CN}\end{array}\right.$,
∴△BFI≌△CIN,
∴BI=CI.
点评 本题主要考查了全等三角形的判定与性质,作辅助线构造全等三角形并熟练运用全等三角形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
17.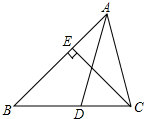 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )
 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
1.为了解某校七年级300名学生的视力情况,从中抽出60名学生进行调查,以下说法正确的是( )
| A. | 该校七年级学生是总体 | B. | 该校七年级的每一个学生是个体 | ||
| C. | 抽出的60名学生是样本 | D. | 样本容量是60 |
 如图,已知Rt△ABC中,AB=AC=3$\sqrt{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD,PE,值△PDE内作第二个内接正方形HIKJ;再取线段JK的中点Q,在△QHI内作第三个内接正方形;…依次进行下去,则第n个内接正方形的面积为$\frac{1}{{4}^{n-2}}$(n为正整数).
如图,已知Rt△ABC中,AB=AC=3$\sqrt{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD,PE,值△PDE内作第二个内接正方形HIKJ;再取线段JK的中点Q,在△QHI内作第三个内接正方形;…依次进行下去,则第n个内接正方形的面积为$\frac{1}{{4}^{n-2}}$(n为正整数).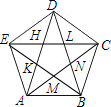 已知:如图,连结正五边形ABCDE各条对角线,就得到一个五角星图案,
已知:如图,连结正五边形ABCDE各条对角线,就得到一个五角星图案,