题目内容
19.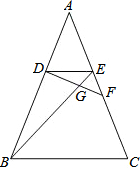 已知:如图,在△ABC中,点D、E分别是AB、AC上的点,且AD=AE,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE,求证:
已知:如图,在△ABC中,点D、E分别是AB、AC上的点,且AD=AE,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE,求证:(1)△DEF∽△BDE;
(2)DG•DF=DB•EF.
分析 (1)根据AD=AE得出∠ADE=∠AED,故∠BDE=∠CED,再由∠EDF=∠ABE可得出结论;
(2)根据△DEF∽△BDE得出$\frac{DB}{DE}$=$\frac{DE}{EF}$,∠BED=∠DFE,故DE2=DB•EF.再由∠GDE=∠EDF得出△GDE∽△EDF,由相似三角形的对应边成比例可得出结论.
解答 证明:(1)∵AD=AE,
∴∠ADE=∠AED,
∴180°-∠ADE=180°-∠AED,即∠BDE=∠CED.
∵∠EDF=∠ABE,
∴△DEF∽△BDE;
(2)∵△DEF∽△BDE,
∴$\frac{DB}{DE}$=$\frac{DE}{EF}$,∠BED=∠DFE,
∴DE2=DB•EF.
∵∠GDE=∠EDF,
∴△GDE∽△EDF,
∴$\frac{DG}{DE}$=$\frac{DE}{DF}$,
∴DE2=DG•DF,
∴DG•DF=DB•EF.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
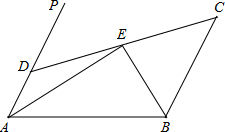 如图,AD∥BC,∠PAB的平分线交于E,CE的延长线交AP于D,求证:AD+BC=AB.
如图,AD∥BC,∠PAB的平分线交于E,CE的延长线交AP于D,求证:AD+BC=AB.