题目内容
14.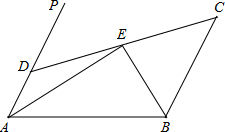 如图,AD∥BC,∠PAB的平分线交于E,CE的延长线交AP于D,求证:AD+BC=AB.
如图,AD∥BC,∠PAB的平分线交于E,CE的延长线交AP于D,求证:AD+BC=AB.
分析 此题要通过构造全等三角形来求解,延长AE交BC的延长线于M;由AP∥BC,及AE平分∠PAB,可求得∠BAE=∠M,即AB=BM,因此直线证得AD=MC即可;在等腰△ABM中,BE是顶角的平分线,根据等腰三角形三线合一的性质知:E是AM的中点,即AE=EM,而PA∥BM,即可证得△ADE≌△MCE,从而得到所求的结论.
解答 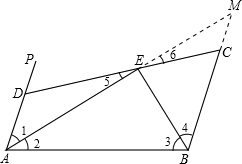 证明:延长AE交BC的延长线于M,
证明:延长AE交BC的延长线于M,
∵AE平分∠PAB,BE平分∠CBA,
∴∠1=∠2,∠3=∠4,
∵AD∥BC
∴∠1=∠M=∠2,∠1+∠2+∠3+∠4=180°
∴BM=BA,∠3+∠2=90°,
∴BE⊥AM,
在△ABE和△MBE中,
$\left\{\begin{array}{l}{∠3=∠4}\\{BE=BE}\\{∠AEB=MEB}\end{array}\right.$
∴△ABE≌△MBE
∴AE=ME,
在△ADE和△MCE中,
$\left\{\begin{array}{l}{∠1=∠M}\\{AE=ME}\\{∠5=∠6}\end{array}\right.$
∴△ADE≌△MCE,
∴AD=CM,
∴AB=BM=BC+AD.
点评 此题主要考查的是全等三角形的判定和性质,同时还涉及了角平分线定义、平行线的性质以及等腰三角形的性质,正确地构造出全等三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.(1)填表
(2)根据发现的规律填空
①已知$\root{3}{3}$=1.442,则$\root{3}{3000}$=14.42,$\root{3}{0.003}$=0.1442
②已知$\root{3}{343}$=7,则$\root{3}{0.000343}$=0.07.
| a | 0.000001 | 0.001 | 1 | 1000 | 1000000 |
| $\root{3}{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
①已知$\root{3}{3}$=1.442,则$\root{3}{3000}$=14.42,$\root{3}{0.003}$=0.1442
②已知$\root{3}{343}$=7,则$\root{3}{0.000343}$=0.07.
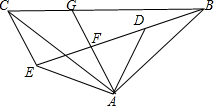 如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,下面结论正确的是①③④(填序号).
如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,下面结论正确的是①③④(填序号).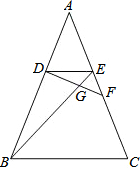 已知:如图,在△ABC中,点D、E分别是AB、AC上的点,且AD=AE,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE,求证:
已知:如图,在△ABC中,点D、E分别是AB、AC上的点,且AD=AE,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE,求证: