题目内容
9.计算(1)(-8)-47+18-(-27)
(2)(-3)×(-9)-8×(-5)
(3)$\frac{9}{2}$×(-$\frac{8}{3}$+2-$\frac{8}{9}$)-|-1|
(4)($\frac{2}{3}$-$\frac{1}{6}$-$\frac{5}{8}$+$\frac{1}{12}$)×(-24)
(5)12÷($\frac{1}{6}$-$\frac{1}{2}$)+2×$\frac{1}{4}$-|$\frac{1}{2}$-3|
分析 (1)先去括号,再根据加法结合律进行计算即可;
(2)先算乘法,再算加减即可;
(3)根据乘法分配律进行计算即可;
(4)根据乘法分配律进行计算即可;
(5)先算括号里面的,再算乘除,最后算加减即可.
解答 解:(1)原式=-8-47+18+27
=-8+18-(47-27)
=10-20
=-10;
(2)原式=27+40
=67;
(3)原式=-$\frac{9}{2}$×$\frac{8}{3}$+$\frac{9}{2}$×2-$\frac{9}{2}$×$\frac{8}{9}$-1
=-12+9-4-1
=-6;
(4)原式=$\frac{2}{3}$×(-24)+$\frac{1}{6}$×24+$\frac{5}{8}$×24-$\frac{1}{12}$×24
=-16+4+15-2
=-12+15-2
=1;
(5)原式=12÷(-$\frac{1}{3}$)+$\frac{1}{2}$-$\frac{5}{2}$
=-36-2
=-38.
点评 本题考查的是有理数的混合运算,熟知有理数混合运算的顺序是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.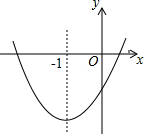 已知二次函数y=ax2+bx+c的图象如图所示(虚线部分是对称轴);则下列结论:
已知二次函数y=ax2+bx+c的图象如图所示(虚线部分是对称轴);则下列结论:
①abc>0;②b=2a;③4ac-b2<0;④a+b+c<0;⑤4a+c<2b;⑥8a+c>0.
其中正确的个数是( )
 已知二次函数y=ax2+bx+c的图象如图所示(虚线部分是对称轴);则下列结论:
已知二次函数y=ax2+bx+c的图象如图所示(虚线部分是对称轴);则下列结论:①abc>0;②b=2a;③4ac-b2<0;④a+b+c<0;⑤4a+c<2b;⑥8a+c>0.
其中正确的个数是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
1.已知x1、x2是一元二次方程x2+2ax+b=0的两个根,且x1+x2=-3,x1x2=-1,则a、b的值分别是( )
| A. | a=-3,b=1 | B. | a=3,b=1 | C. | a=$\frac{3}{2}$,b=-1 | D. | a=-$\frac{3}{2}$,b=1 |
18.下列各式从左到右的变形是因式分解的是( )
| A. | (a+1)(a-1)=a2-1 | B. | x2-4x+5=x(x-4)+5 | C. | 3x2-6x=-6x+3x2 | D. | 8a-4a2-4=-4(a-1)2 |
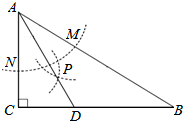 如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )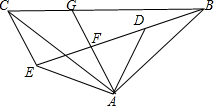 如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,下面结论正确的是①③④(填序号).
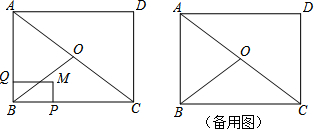
如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,下面结论正确的是①③④(填序号).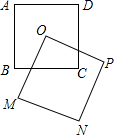 如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,这两个正方形重叠部分的面积为25.
如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,这两个正方形重叠部分的面积为25.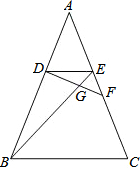 已知:如图,在△ABC中,点D、E分别是AB、AC上的点,且AD=AE,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE,求证:
已知:如图,在△ABC中,点D、E分别是AB、AC上的点,且AD=AE,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE,求证: