题目内容
11．甲、乙、丙分别在数轴的-20、+30、原点处，他们在数轴运行的速度分别为1米/秒、2米/秒、3米/秒．若甲、乙相向而行，在甲、乙出发时丙也同时出发．且丙先遇甲后立即回头再遇乙，求乙、丙相遇点表示的数？分析 设甲、丙经过x秒相遇，根据题意得到x+3x=20，从而可求得x=5，故此可求得丙、乙所在位置表示的数，然后设甲、丙相遇后y秒，乙、丙相遇根据乙行驶的路程+丙行驶的路程=35列方程求解即可．
解答 解：设甲、丙经过x秒相遇．
根据题意可知：x+3x=20，
解得：x=5．
∵-5×3=-15，30-2×5=20，
∴此时丙的位于-15处，乙位于20处．
设甲、丙相遇后y秒，乙、丙相遇．
根据题意得：2y+3y=20-（-15），
解得：y=7．
20-2×7=6．
答：乙、丙相遇点表示的数是6．
点评 本题主要考查的是一元一次方程的应用，找出题目的相等关系是解题的关键．
练习册系列答案
相关题目
1．已知x1、x2是一元二次方程x2+2ax+b=0的两个根，且x1+x2=-3，x1x2=-1，则a、b的值分别是（ ）
| A． | a=-3，b=1 | B． | a=3，b=1 | C． | a=$\frac{3}{2}$，b=-1 | D． | a=-$\frac{3}{2}$，b=1 |
2．（1）填表
（2）根据发现的规律填空
①已知$\root{3}{3}$=1.442，则$\root{3}{3000}$=14.42，$\root{3}{0.003}$=0.1442
②已知$\root{3}{343}$=7，则$\root{3}{0.000343}$=0.07．
| a | 0.000001 | 0.001 | 1 | 1000 | 1000000 |
| $\root{3}{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
①已知$\root{3}{3}$=1.442，则$\root{3}{3000}$=14.42，$\root{3}{0.003}$=0.1442
②已知$\root{3}{343}$=7，则$\root{3}{0.000343}$=0.07．
19．
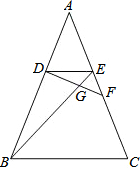已知：如图，在△ABC中，点D、E分别是AB、AC上的点，且AD=AE，点F在边AC上，DF与BE相交于点G，且∠EDF=∠ABE，求证：
（1）△DEF∽△BDE；
（2）DG•DF=DB•EF．
已知：如图，在△ABC中，点D、E分别是AB、AC上的点，且AD=AE，点F在边AC上，DF与BE相交于点G，且∠EDF=∠ABE，求证：（1）△DEF∽△BDE；
（2）DG•DF=DB•EF．
20．下列各式中，变形正确的是（ ）
| A． | $\frac{x}{y}=\frac{x+y}{2y}$ | B． | $\frac{m+b}{a-b}=\frac{m+1}{a-1}$ | C． | $\frac{a}{b}=\frac{a•m}{b•m}$ | D． | $\frac{{x}^{2}-{y}^{2}}{y+x}=x-y$ |