题目内容
2.己知抛物线y=x2+bx+c经过点(-1,0)和(3,0).(1)求抛物线的函数表达式;
(2)求抛物线的顶点,并指出抛物线的开口方向和对称轴.
分析 (1)把点(-1,0)和(3,0)代入抛物线y=x2+bx+c即可得出答案;
(2)根据顶点的坐标公式(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)求得抛物线的顶点和对称轴,根据a的符号得出抛物线的开口方向.
解答 解:(1)把点(-1,0)和(3,0)代入抛物线y=x2+bx+c,
得$\left\{\begin{array}{l}{1-b+c=0}\\{9+3b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
∴抛物线的函数表达式为y=x2-2x-3;
(2)-$\frac{b}{2a}$=-$\frac{-2}{2}$=1,$\frac{4ac-{b}^{2}}{4a}$=$\frac{-12-4}{4}$=-4,
∴点的坐标(1,-4),
∵a=1>0,
∴抛物线开口向上,
对称轴为直线x=1.
点评 本题考查了用待定系数法求二次函数的解析式,掌握点的坐标的求法,对称轴的求法以及开口方向的判定是解题的关键.

练习册系列答案
相关题目
12.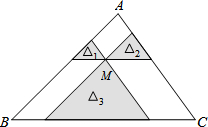 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )
 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )| A. | 62 | B. | 186 | C. | 132 | D. | 144 |
10. 我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过市场调查,得到如下数据:
我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过市场调查,得到如下数据:
(1)把上表中x、y的各组对应值作为点的坐标,在给出的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式及自变量x的取值范围;
(2)若市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
 我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过市场调查,得到如下数据:
我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过市场调查,得到如下数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |
(2)若市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
14.某人下午6点到7点之间外出购物,出发和回来时发现表上的时针和分针的夹角都为110°,此人外出购物共用了( )分钟.
| A. | 16 | B. | 20 | C. | 32 | D. | 40 |
 油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片102片或者长方形铁片80片,如图,一个油桶由两个圆形铁片和一个长方形铁片相配套,生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?
油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片102片或者长方形铁片80片,如图,一个油桶由两个圆形铁片和一个长方形铁片相配套,生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套? 如图,△ABC中,AC=13,AB=12,BC=5,CD是△ABC的角平分线,DE⊥AC于E,连结EB.
如图,△ABC中,AC=13,AB=12,BC=5,CD是△ABC的角平分线,DE⊥AC于E,连结EB.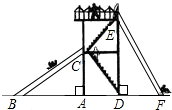 如图有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,求∠FED和∠EFD的度数.
如图有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,求∠FED和∠EFD的度数.