题目内容
12.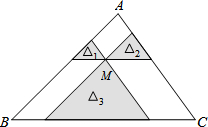 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中的阴影部分)的面积是4,9,49,则△ABC的面积是( )| A. | 62 | B. | 186 | C. | 132 | D. | 144 |
分析 先利用相似三角形的判定方法易得△1∽△2∽△3∽△ABC,则利用相似三角形的性质得EF:DM:MH=2:3:7,再利用四边形ADME和四边形FMHB为平行四边形得到AE=DM,FB=MH,所以AE:EF:FB=2:3:7,于是得到EF:AB=1:6,然后根据相似三角形的性质求S△ABC.
解答 解:∵过点M分别作直线平行于△ABC的各边,
∴△1∽△2∽△3∽△ABC,
∵△1,△2,△3(图中的阴影部分)的面积是4,9,49,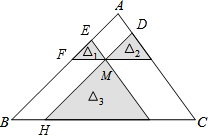
∴EF:DM:MH=2:3:7,
易得四边形ADME和四边形FMHB为平行四边形,
∴AE=DM,FB=MH,
∴AE:EF:FB=2:3:7,
∴EF:AB=2:12=1:6,
∴S△1:S△ABC=1:36,
∴S△ABC=36×4=144.
故选D.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;熟练掌握应用相似三角形的性质是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,观察图象,判断下列说法错误的是( )
如图,观察图象,判断下列说法错误的是( )
 如图,观察图象,判断下列说法错误的是( )
如图,观察图象,判断下列说法错误的是( )| A. | 方程组$\left\{\begin{array}{l}y=2x-1\\ y=-\frac{3}{5}x+\frac{8}{5}\end{array}\right.$.的解是 $\left\{\begin{array}{l}x=1\\ y=1.\end{array}\right.$ | |
| B. | 不等式-$\frac{3}{5}$x+$\frac{8}{5}$≤2x-1的解集是x≥1 | |
| C. | 不等式-$\frac{3}{5}$x+$\frac{8}{5}$>2x-1的解集是x>1 | |
| D. | 方程-$\frac{3}{5}$x+$\frac{8}{5}$=2x-1的解是x=1 |
7.网购已成为人们购物的一种方式,2015年双11仅阿里巴巴交易额就超过912亿元,用科学记数法表示数912亿是( )
| A. | 9.12×109 | B. | 9.12×1010 | C. | 9.12×108 | D. | 9.12×1011 |
4.在Rt△OAB中,∠OAB=15°,OC为斜边上的高,且OC=1,P,Q分别为△AOC和△BOC的内心(内心为三角形三条角平分线的交点),连接PQ并延长交OB于M,则OM=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为E,F.
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为E,F. 如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.