题目内容
 在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F,求证:AE=CF.
在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F,求证:AE=CF.考点:平行四边形的性质
专题:证明题
分析:由条件可证明四边形BEDF为平行四边形,可得到BE=DF,结合平行四边形的性质可求得AE=CF.
解答:证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=DC,
又∵DE⊥AB,BF⊥CD,
∴∠DEB=∠BFD=90°,且∠BED+∠EDF=180°,
∴∠BFD+∠EDF=180°,
∴DE∥BF,
∴四边形BEDF为平行四边形,
∴BE=DF,
∴AB-BE=CD-DF,
即AE=CF.
∴AB∥CD,AB=DC,
又∵DE⊥AB,BF⊥CD,
∴∠DEB=∠BFD=90°,且∠BED+∠EDF=180°,
∴∠BFD+∠EDF=180°,
∴DE∥BF,
∴四边形BEDF为平行四边形,
∴BE=DF,
∴AB-BE=CD-DF,
即AE=CF.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
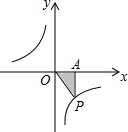 如图,P是反比例函数图象上的一点,过点P向x轴作垂线,垂足为A,若△PAO的面积为4,则这个反比例函数的解析式为( )
如图,P是反比例函数图象上的一点,过点P向x轴作垂线,垂足为A,若△PAO的面积为4,则这个反比例函数的解析式为( )A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
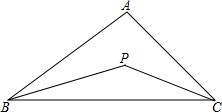 如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y
如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y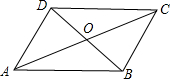 如图,在?ABCD中,∠DAC=30°,∠DOC=120°,OA=6cm,OB=3cm.求AD与AB的长.
如图,在?ABCD中,∠DAC=30°,∠DOC=120°,OA=6cm,OB=3cm.求AD与AB的长. 用小立方体搭几何体,主视图和俯视图如图所示,这样的几何正方体最少需要
用小立方体搭几何体,主视图和俯视图如图所示,这样的几何正方体最少需要