题目内容
19.如图,A点的初始位置位于数轴上表示1的点,现对A点做如下移动:第1次向左移动3个单位长度至B点,第2次从B点向右移动6个单位长度至C点,第3次从C点向左移动9个单位长度至D点,第4次从D点向右移动12个单位长度至E点,…,以此类推,则点E在数轴上所表示的数为7,这样第1343次移动到的点到原点的距离为2015.
分析 根据数轴上点的坐标变化和平移规律(左减右加),分别求出点所对应的数,进而求出点到原点的距离;然后对奇数项、偶数项分别探究,找出其中的规律(相邻两数都相差3),写出表达式就可解决问题.
解答 解:第1次点A向左移动3个单位长度至点B,则B表示的数,1-3=-2;
第2次从点B向右移动6个单位长度至点C,则C表示的数为-2+6=4;
第3次从点C向左移动9个单位长度至点D,则D表示的数为4-9=-5;
第4次从点D向右移动12个单位长度至点E,则点E表示的数为-5+12=7;
第5次从点E向左移动15个单位长度至点F,则F表示的数为7-15=-8;
…;
由以上数据可知,当移动次数为奇数时,点在数轴上所表示的数满足:-$\frac{1}{2}$(3n+1),
当移动次数为偶数时,点在数轴上所表示的数满足:3n-2,
当移动次数为奇数时,-$\frac{1}{2}$(3n+1)=-2015,n=1343,
当移动次数为偶数时,3n-2=2015,n=$\frac{2017}{3}$(不合题意),
故答案为:7;1343.
点评 本题考查了数轴,以及用正负数可以表示具有相反意义的量,还考查了数轴上点的坐标变化和平移规律(左减右加),考查了一列数的规律探究.对这列数的奇数项、偶数项分别进行探究是解决这道题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
14.当x=( )时,分式$\frac{{{x^2}-1}}{x-1}$的值为零.
| A. | 0 | B. | 1 | C. | ±1 | D. | -1 |
8.某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:如果公司认为,作为公关人员面试的成绩比笔试的成绩更重要,并分别赋予它们6和4的权,根据四人各自的平均成绩,公司将录取乙.
| 候选人 | 甲 | 乙 | 丙 | 丁 | |
| 测试成绩(百分制) | 面试 | 86 | 92 | 90 | 83 |
| 笔试 | 90 | 83 | 83 | 92 | |
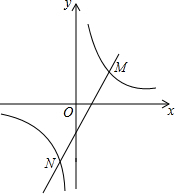 如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象交于点M(2,m)、N(-1,-4)两点,则kx+b>$\frac{a}{x}$的解集为x<-1或x>2.
如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象交于点M(2,m)、N(-1,-4)两点,则kx+b>$\frac{a}{x}$的解集为x<-1或x>2.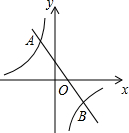 如图,在直角坐标系中,一次函数y=-x+b与反比例函数y=$\frac{-4}{x}$的图象交于A,B两点,已知A(-1,a).
如图,在直角坐标系中,一次函数y=-x+b与反比例函数y=$\frac{-4}{x}$的图象交于A,B两点,已知A(-1,a).