题目内容
4.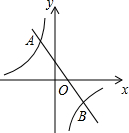 如图,在直角坐标系中,一次函数y=-x+b与反比例函数y=$\frac{-4}{x}$的图象交于A,B两点,已知A(-1,a).
如图,在直角坐标系中,一次函数y=-x+b与反比例函数y=$\frac{-4}{x}$的图象交于A,B两点,已知A(-1,a).(1)求一次函数的解析式;
(2)求B点的坐标;
(3)结合图象,直接写出当-x+b>$\frac{-4}{x}$时,x的取值范围.
分析 (1)把A(-1,a)代入y=$\frac{-4}{x}$求出a,得到点A的坐标,把点A的坐标代入y=-x+b求出b,得到一次函数的解析式;
(2)把解出的一次函数y=-x+b与反比例函数y=$\frac{-4}{x}$组成方程组,解方程组得到答案;
(3)根据函数图象确定当-x+b>$\frac{-4}{x}$时,x的取值范围.
解答 解:(1)∵A(-1,a)在y=$\frac{-4}{x}$的图象上,
∴a=4,则A(-1,4),
又A(-1,4)在一次函数y=-x+b图象上,
∴1+b=4,解得,b=3,
∴一次函数的解析式为:y=-x+3;
(2)由题意得,$\left\{\begin{array}{l}{y=-x+3}\\{y=-\frac{4}{x}}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2}=-1}\end{array}\right.$,
∴B点的坐标为:(4,-1);
(3)从图象可以看出,当x<-1或0<x<4时,-x+b>$\frac{-4}{x}$.
点评 本题综合考查一次函数与反比例函数的图象与性质,同时考查用待定系数法求函数解析式,先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列图形中不一定是轴对称图形的是( )
| A. | 线段 | B. | 角 | C. | 三角形 | D. | 圆 |
16.以方程组$\left\{\begin{array}{l}{3x+4y=-1}\\{3x-y=-11}\end{array}\right.$的解为坐标的点P(x,y)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.在平面直角坐标系中,点P(-3,0)在( )
| A. | x轴上 | B. | y轴上 | C. | 第三象限 | D. | 第四象限 |
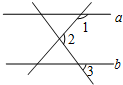 如图,直线a∥b,∠1=130°,∠2=110°,则∠3的度数是60度.
如图,直线a∥b,∠1=130°,∠2=110°,则∠3的度数是60度. 如图,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,且∠DEC=90°,试判断AD与BC的位置关系,并说明理由.
如图,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,且∠DEC=90°,试判断AD与BC的位置关系,并说明理由.
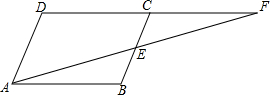 如图,在平行四边形ABCD中,E为BC的中点,AE的延长线与DC的延长线相交于F.
如图,在平行四边形ABCD中,E为BC的中点,AE的延长线与DC的延长线相交于F.