题目内容
9.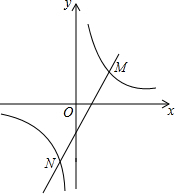 如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象交于点M(2,m)、N(-1,-4)两点,则kx+b>$\frac{a}{x}$的解集为x<-1或x>2.
如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象交于点M(2,m)、N(-1,-4)两点,则kx+b>$\frac{a}{x}$的解集为x<-1或x>2.
分析 根据图象可知,不等式kx+b>$\frac{a}{x}$的解集即为一次函数图象在反比例函数图象的上方时对应的x的范围,结合M、N点的横坐标可得出答案.
解答 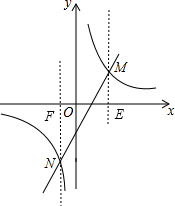 解:
解:
根据函数图象可知,不等式kx+b>$\frac{a}{x}$的解集为一次函数图象在反比例函数图象上方时对应的x的值,
如图,过M作ME⊥x轴,过N作NF⊥x轴,垂足分别为E、F,
则可知当x的值在直线ME右侧或在直线NF左侧时满足条件,
∵M(2,m)、N(-1,-4),
∴不等式的解集为x<-1或x>2,
故答案为:x<-1或x>2.
点评 本题主要考查一次函数与反比例函数的交点,把不等式问题转化为函数图象的关系是解题的关键,注意数形结合思想的应用.

练习册系列答案
相关题目
4.已知关于x的方程(x-1)[(k-1)x+(k-3)]=0(k是常数),则下列说法中正确的是( )
| A. | 方程一定有两个不相等的实数根 | B. | 方程一定有两个实数根 | ||
| C. | 当k取某些值时,方程没有实数根 | D. | 方程一定有实数根 |
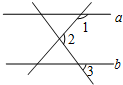 如图,直线a∥b,∠1=130°,∠2=110°,则∠3的度数是60度.
如图,直线a∥b,∠1=130°,∠2=110°,则∠3的度数是60度.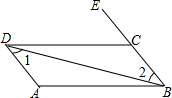 如图:由∠1=∠2,可以得出AD∥BC,理由是内错角相等,两直线平行;
如图:由∠1=∠2,可以得出AD∥BC,理由是内错角相等,两直线平行;