题目内容
9.阅读填空:(1)请你阅读芳芳的说理过程并填出理由:
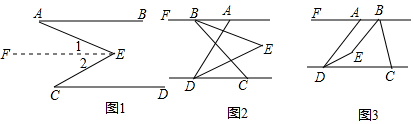
如图1,已知AB∥CD.
求证:∠BAE+∠DCE=∠AEC.
理由:作EF∥AB,则有EF∥CD(平行于同一条直线的两条直线平行)
∴∠1=∠BAE,∠2=∠DCE(两直线平行,内错角相等)
∴∠AEC=∠1+∠2=∠BAE+∠DCE(等量代换)
思维拓展:
(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC.BE、DE所在直线交于点E,若∠FAE=m°,∠ABC=n°,求∠BED的度数.(用含m、n的式子表示)
(3)将图2中的线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,得到图3,直接写出∠BED的度数是180°-$\frac{1}{2}$n°+$\frac{1}{2}$m°(用含m、n的式子表示).
分析 (1)根据平行线的性质即可得到结论;
(2)先过点E作EH∥AB,根据平行线的性质和角平分线的定义,即可得到结论;
(3)过E作EG∥AB,根据平行线的性质和角平分线的定义,即可得到结论.
解答 解:阅读填空:
(1)平行于同一条直线的两条直线平行;
两直线平行,内错角相等;
等量代换,
故答案为:平行于同一条直线的两条直线平行,两直线平行,内错角相等,等量代换;
思维拓展:
(2)如图2,过点E作EH∥AB,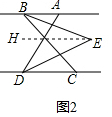
∵AB∥CD,∠FAD=m°,
∴∠FAD=∠ADC=m°,
∵DE平分∠ADC,∠ADC=m°,.
∴∠EDC=$\frac{1}{2}$∠ADC=$\frac{1}{2}$m°,
∵BE平分∠ABC,∠ABC=n°,
∴∠ABE=$\frac{1}{2}$∠ABC=$\frac{1}{2}$n°,
∵AB∥CD,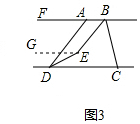
∴AB∥CD∥EH,
∴∠ABE=∠BEH=$\frac{1}{2}$n°,∠CDE=∠DEH=$\frac{1}{2}$m°,
∴∠BED=∠BEH+∠DEH=$\frac{1}{2}$n°+$\frac{1}{2}$m°=$\frac{1}{2}$( n°+m°);
(3)∠BED的度数改变.
过点E作EG∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=∠GAD=m°
∴∠ABE=$\frac{1}{2}$∠ABC=$\frac{1}{2}$n°,∠CDE=$\frac{1}{2}$∠ADC=$\frac{1}{2}$m°
∵AB∥CD,
∴AB∥CD∥EG,
∴∠BEG=180°-∠ABE=180°-$\frac{1}{2}$n°,∠CDE=∠DEG=$\frac{1}{2}$m°,
∴∠BED=∠BEG+∠DEG=180°-$\frac{1}{2}$n°+$\frac{1}{2}$m°.
故答案为:180°-$\frac{1}{2}$n°+$\frac{1}{2}$m°.
点评 本题主要考查了平移的性质,平行线的性质以及角平分线的定义的运用,解决问题的关键是正确的作出辅助线.

| A. | 4<m<5 | B. | 4≤m<5 | C. | 4<m≤5 | D. | 4≤m≤5 |
| A. |  | B. |  | C. |  | D. |  |
| A. | x≠-1 | B. | x<1 | C. | x≤1 | D. | x≥1 |
 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.