题目内容
14. 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-$\frac{6}{x}$<0的x的取值范围.
分析 (1)将A、B坐标代入双曲线解析式求得m、n的值,即可知A、B坐标,再根据待定系数法求解即可.
(2)该不等式的解集即为直线在双曲线下方时x的范围.
解答 解:(1)将A(m,6),B(3,n)两点分别代入y=$\frac{6}{x}$,
得:m=1,n=2,
则点A(1,6)、B(3,2),
将点A、B坐标代入y=kx+b得:$\left\{\begin{array}{l}{k+b=6}\\{3k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=8}\end{array}\right.$,
∴一次函数的解析式为y=-2x+8;
(2)由图象可知是0<x<1或x>3,
即kx+b-$\frac{6}{x}$<0的解集为0<x<1或x>3.
点评 本题主要考查双曲线与直线的交点问题,熟练掌握待定系数法求函数解析式和数形结合思想的运用是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
2.已知x=1,y=2是方程kx-2y-1=0的解,则k的值为( )
| A. | 5 | B. | -5 | C. | 3 | D. | -3 |
6.已知xb+2-2ya-1=2是关于x、y的二元一次方程,则a、b的值分别是( )
| A. | a=2,b=1 | B. | a=3,b-2 | C. | a=2,b=-1 | D. | a=-1,b=2 |
3.已知y是x的一次函数,下表列出了部分y与x的对应值.
则m的值为-1.
| x | -2 | 0 | 1 | 3 |
| y | -5 | m | 1 | 5 |
2.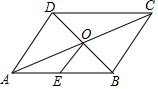 如图,在?ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=5,则BC的长为( )
如图,在?ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=5,则BC的长为( )
 如图,在?ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=5,则BC的长为( )
如图,在?ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=5,则BC的长为( )| A. | 10 | B. | 9 | C. | 8 | D. | 5 |
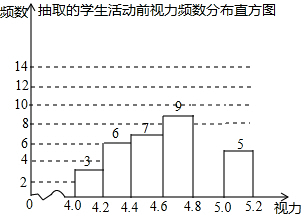 为了保护视力,学校计划开展“爱眼护眼”视力保健活动,为使活动更具有实效性,先对学生视力情况进行调查,随机抽取40名学生,检查他们的视力,并绘制不完整的直方图(数据包括左端点不包括右端点,精确到0.1),请结合直方图的信息解答下列问题:
为了保护视力,学校计划开展“爱眼护眼”视力保健活动,为使活动更具有实效性,先对学生视力情况进行调查,随机抽取40名学生,检查他们的视力,并绘制不完整的直方图(数据包括左端点不包括右端点,精确到0.1),请结合直方图的信息解答下列问题: