若关于x的不等式$\left\{\begin{array}{l}{x-m＜0}\\{7-2x≤1}\end{array}\right.$的整数解共有2个.则m的取值范围是( )A．4＜m＜5B．4≤m＜5C．4＜m≤5D．4≤m≤5 题目和参考答案——青夏教育精英家教网—

题目内容

2．若关于x的不等式$\left\{\begin{array}{l}{x-m＜0}\\{7-2x≤1}\end{array}\right.$的整数解共有2个，则m的取值范围是（　　）

A．

4＜m＜5

B．

4≤m＜5

C．

4＜m≤5

D．

4≤m≤5

分析表示出不等式组的解集，由整数解有2个，确定出m的范围即可．

解答解：不等式组整理得：$\left\{\begin{array}{l}{x＜m}\\{x≥3}\end{array}\right.$，即3≤x＜m，
由不等式的整数解有2个，得到整数解为3，4，
则m的范围为4＜m≤5．
故选C

点评此题考查了一元一次不等式组的整数解，求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．

练习册系列答案

相关题目

13．下列给出的条件中，能判定四边形ABCD是平行四边形的是（　　）

14．一次函数y=（2m-6）x+4中，y随x的增大而减小，则m的取值范围是m＜3．

11．一次函数y=（m-2）x+m²的图象过（0，4），则m=-2．

7．

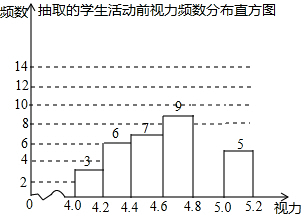为了保护视力，学校计划开展“爱眼护眼”视力保健活动，为使活动更具有实效性，先对学生视力情况进行调查，随机抽取40名学生，检查他们的视力，并绘制不完整的直方图（数据包括左端点不包括右端点，精确到0.1），请结合直方图的信息解答下列问题：
（1）统计图中，4.8≤x＜5.0的学生数是10人；
（2）将频数分布直方图补充完整；
（3）若绘制“学生视力扇形统计图”，视力达到4.8及以上为达标，则视为达标学生所对应扇形的圆心角度数为135°；
（4）若全校共有800名学生，则视力达标的学生估计有300名．

13．计算：3$\sqrt{5}+2\sqrt{\frac{1}{2}}-\sqrt{20}-\frac{1}{2}\sqrt{32}$．

9．阅读填空：
（1）请你阅读芳芳的说理过程并填出理由：
如图1，已知AB∥CD．
求证：∠BAE+∠DCE=∠AEC．
理由：作EF∥AB，则有EF∥CD（平行于同一条直线的两条直线平行）
∴∠1=∠BAE，∠2=∠DCE（两直线平行，内错角相等）
∴∠AEC=∠1+∠2=∠BAE+∠DCE（等量代换）
思维拓展：
（2）如图2，已知AB∥CD，BE平分∠ABC，DE平分∠ADC．BE、DE所在直线交于点E，若∠FAE=m°，∠ABC=n°，求∠BED的度数．（用含m、n的式子表示）
（3）将图2中的线段BC沿DC方向平移，使得点B在点A的右侧，其他条件不变，得到图3，直接写出∠BED的度数是180°-$\frac{1}{2}$n°+$\frac{1}{2}$m°（用含m、n的式子表示）．

10．下列变形中，正确的是（　　）

A．

-$\frac{1}{a}$=$\frac{-1}{a}$

B．

$\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{a+b}$

C．

$\frac{2{b}^{2}}{{a}^{2}}$=$\frac{2b}{a}$

D．

$\frac{a+ab}{b+ab}$=$\frac{a}{b}$

试题分类