题目内容
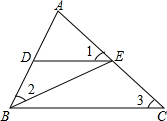 如图所示,∠1=∠2=∠3,请找出所有相似三角形.
如图所示,∠1=∠2=∠3,请找出所有相似三角形.考点:相似三角形的判定
专题:
分析:由∠1=∠3可知DE∥BC,结合条件可找相似的三角形.
解答:解:
∵∠1=∠2,且∠DAE=∠EAB,
∴△ADE∽△AEB,
∵∠1=∠3,且∠DAE=∠BAC,
∴△ADE∽△ABC,
∵∠1=∠3,
∴DE∥BC,
∴∠DEB=∠EBC,且∠2=∠3,
∴△DEB∽△EBC,
∵∠2=∠3,且∠BAE=∠CAB,
∴△AEB∽△ABC,
综上可知相似三角形有△ADE和△AEB、△ADE和△ABC、△DEB和△EBC、△AEB和△ABC
∵∠1=∠2,且∠DAE=∠EAB,
∴△ADE∽△AEB,
∵∠1=∠3,且∠DAE=∠BAC,
∴△ADE∽△ABC,
∵∠1=∠3,
∴DE∥BC,
∴∠DEB=∠EBC,且∠2=∠3,
∴△DEB∽△EBC,
∵∠2=∠3,且∠BAE=∠CAB,
∴△AEB∽△ABC,
综上可知相似三角形有△ADE和△AEB、△ADE和△ABC、△DEB和△EBC、△AEB和△ABC
点评:本题主要考查相似三角形的判定,掌握有两组角对应相等的三角形相似是解题的关键.

练习册系列答案
相关题目
一个角和它的余角的比是1:2,则这个角的补角的度数是( )
| A、150° | B、120° |
| C、110° | D、70° |
已知⊙O上有一点A,直线l经过点A,则l与⊙O的位置关系是( )
| A、相切 | B、相交 |
| C、相离 | D、相交或相切 |
 如图,线段AB=6,点O是线段AB上一点,C,D分别是线段OA,OB的中点,小华据此轻松地求得CD=3.他在反思过程中突发奇想:若点O运动到AB的延长线上,原有的结论“CD=3”是否仍然成立?请帮小华画出图形并说明理由.
如图,线段AB=6,点O是线段AB上一点,C,D分别是线段OA,OB的中点,小华据此轻松地求得CD=3.他在反思过程中突发奇想:若点O运动到AB的延长线上,原有的结论“CD=3”是否仍然成立?请帮小华画出图形并说明理由.