题目内容
已知△ABC,点E在直线AB上,点D在直线AC上,且BD=AE,过点E作EG∥BC交直线BD于点G,交直线AC于点F,且BG=AB,∠ABG=60°.
(1)当点D在线段AC上时如图①,求证:EG=BC+DF;
(2)当点D在线段AC延长线上时,如图②;当点D在线段CA延长线上时,如图③,请分别写出线段EG、BC、DF之间的数量关系,不需要证明.
(3)若∠BAC=30°,AB=3
,则DF= .
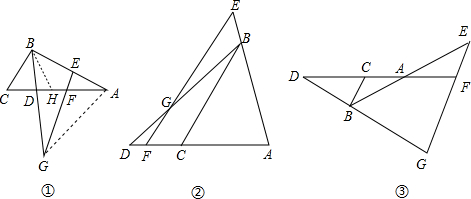
(1)当点D在线段AC上时如图①,求证:EG=BC+DF;
(2)当点D在线段AC延长线上时,如图②;当点D在线段CA延长线上时,如图③,请分别写出线段EG、BC、DF之间的数量关系,不需要证明.
(3)若∠BAC=30°,AB=3
| 3 |

考点:全等三角形的判定与性质
专题:
分析:(1)在AC上找到H点使得BH=BC,连接AG,易证△ABG为等边三角形,根据等边三角形性质可证明△ABD≌△GAE,可得EG=AD,再根据△BCH为等边三角形,即可证明△ABH≌△GAF,可得AF=BC,即可解题;
(2)①延长DA至H使得BH=BD,连接AG,根据△ABG是等边三角形可证明△DBA≌△EAG,可得AD=EG,∠DAB=∠AGE,再证明△CBH≌△FAE,可得BC=AF,即可解题;
②连接AG,根据△ABG是等边三角形,可证明△DBA≌△EAG,可得AD=EG,∠DAB=∠AGE,即可证明△DCB∽△DGA和△EAF∽△AGE,根据相似三角形对应边比例相等可得AF=BC,即可解题;
(3)根据∠BAC=30°画出图形,易证∠D=30°,可得BD=2AC,再根据AF=BC,即可求得DF的长,即可解题.
(2)①延长DA至H使得BH=BD,连接AG,根据△ABG是等边三角形可证明△DBA≌△EAG,可得AD=EG,∠DAB=∠AGE,再证明△CBH≌△FAE,可得BC=AF,即可解题;
②连接AG,根据△ABG是等边三角形,可证明△DBA≌△EAG,可得AD=EG,∠DAB=∠AGE,即可证明△DCB∽△DGA和△EAF∽△AGE,根据相似三角形对应边比例相等可得AF=BC,即可解题;
(3)根据∠BAC=30°画出图形,易证∠D=30°,可得BD=2AC,再根据AF=BC,即可求得DF的长,即可解题.
解答:(1)证明:在AC上找到H点使得BH=BC,连接AG,
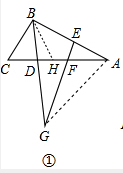
∵AB=BG,∠ABD=60°,
∴△ABG为等边三角形,
∴∠BAG=60°,AG=AB,
在△ABD和△GAE中,
,
∴△ABD≌△GAE,(SAS)
∴∠AGE=∠BAD,EG=AD,∠AEG=∠ADB,
∵∠AEG+∠AFE+∠EAF=180°,∠ADB+∠ABD+∠EAF=180°,
∴∠AFE=∠ABD=60°,
∵EG∥BC,
∴∠C=60°,
∵BH=BC,
∴△BCH为等边三角形,
∴BH=BC,∠AHB=120°,
在△ABH和△GAF中,
,
∴△ABH≌△GAF,(AAS)
∴AF=BH,
∴AF=BC,
∵AD=AF+DF,
∴EG=BC+DF;
(2)证明:①延长DA至H使得BH=BD,连接AG,
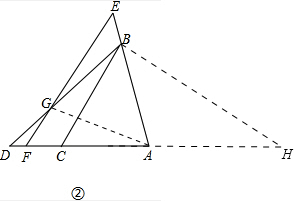
∵BH=BD,
∴∠H=∠D,AE=BH,
∵∠ABG=60°,BG=AB,
∴△ABG是等边三角形,
∴AB=AG,∠ABG=∠BAG=60°,
在△BDA和△AEG中,
,
∴△BDA≌△AEG(SAS),
∴EG=AD,∠E=∠D,
∴∠H=∠D,
∵BC∥EF,
∴∠BCA=∠EFC,
在△CBH和△FAE中,
,
∴△CBH≌△FAE(AAS),
∴BC=AF,
∵AD=AF+DF,
∴EG=BC+DF;
②连接AG,
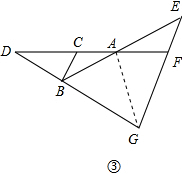
∵∠ABG=60°,BG=AB,
∴△ABG是等边三角形,
∴AB=AG,∠ABG=∠BAG=60°,
∴∠DBA=∠EAG=120°,
在△DBA和△EAG中,
,
∴△DBA≌△EAG,(SAS)
∴AD=EG,∠DAB=∠AGE,
∵∠CBA=∠E,∠E+∠AGE=60°,
∴∠DCB=∠CBA+∠DAB=∠E+∠AGE=∠BAG=60°,
∴△DCB∽△DGA,
∴
=
,
∵∠EAF=∠DAB,∠DAB=∠AGE,
∴∠EAF=∠AGE,
∴△EAF∽△AGE,
∴
=
,
∵BD=AE,AD=EG,
∴
=
,
∴AF=BC,
∵DF=AF+AD,
∴DF=BC+EG;
(3)解:根据∠BAC=30°画出图形,
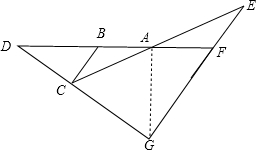
∵∠AGE=∠BAC,∠BAC+∠D=60°,
∴∠CGF=90°,∠D=30°,
∵BC∥GF,∴∠CBD=60°,
∴∠ACB=30°,
∴BC=AC,BD=2BC=2AC,
∵AF=BC,
∴DF=AD+AF=AB+BD+AF=4AB=12
.

∵AB=BG,∠ABD=60°,
∴△ABG为等边三角形,
∴∠BAG=60°,AG=AB,
在△ABD和△GAE中,
|
∴△ABD≌△GAE,(SAS)
∴∠AGE=∠BAD,EG=AD,∠AEG=∠ADB,
∵∠AEG+∠AFE+∠EAF=180°,∠ADB+∠ABD+∠EAF=180°,
∴∠AFE=∠ABD=60°,
∵EG∥BC,
∴∠C=60°,
∵BH=BC,
∴△BCH为等边三角形,
∴BH=BC,∠AHB=120°,
在△ABH和△GAF中,
|
∴△ABH≌△GAF,(AAS)
∴AF=BH,
∴AF=BC,
∵AD=AF+DF,
∴EG=BC+DF;
(2)证明:①延长DA至H使得BH=BD,连接AG,

∵BH=BD,
∴∠H=∠D,AE=BH,
∵∠ABG=60°,BG=AB,
∴△ABG是等边三角形,
∴AB=AG,∠ABG=∠BAG=60°,
在△BDA和△AEG中,
|
∴△BDA≌△AEG(SAS),
∴EG=AD,∠E=∠D,
∴∠H=∠D,
∵BC∥EF,
∴∠BCA=∠EFC,
在△CBH和△FAE中,
|
∴△CBH≌△FAE(AAS),
∴BC=AF,
∵AD=AF+DF,
∴EG=BC+DF;
②连接AG,

∵∠ABG=60°,BG=AB,
∴△ABG是等边三角形,
∴AB=AG,∠ABG=∠BAG=60°,
∴∠DBA=∠EAG=120°,
在△DBA和△EAG中,
|
∴△DBA≌△EAG,(SAS)
∴AD=EG,∠DAB=∠AGE,
∵∠CBA=∠E,∠E+∠AGE=60°,
∴∠DCB=∠CBA+∠DAB=∠E+∠AGE=∠BAG=60°,
∴△DCB∽△DGA,
∴
| BC |
| AG |
| BD |
| AD |
∵∠EAF=∠DAB,∠DAB=∠AGE,
∴∠EAF=∠AGE,
∴△EAF∽△AGE,
∴
| AF |
| AG |
| AE |
| EG |
∵BD=AE,AD=EG,
∴
| BC |
| AG |
| AF |
| AG |
∴AF=BC,
∵DF=AF+AD,
∴DF=BC+EG;
(3)解:根据∠BAC=30°画出图形,

∵∠AGE=∠BAC,∠BAC+∠D=60°,
∴∠CGF=90°,∠D=30°,
∵BC∥GF,∴∠CBD=60°,
∴∠ACB=30°,
∴BC=AC,BD=2BC=2AC,
∵AF=BC,
∴DF=AD+AF=AB+BD+AF=4AB=12
| 3 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,考查了相似三角形的判定和相似三角形对应边比例相等的性质,本题中求证△DBA≌△EAG是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
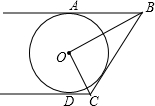 已知:如图,AB、CD是⊙O的两条平行切线,A、C是切点,⊙O的另一条切线BD与
已知:如图,AB、CD是⊙O的两条平行切线,A、C是切点,⊙O的另一条切线BD与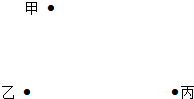 作图题:如图,现在甲、乙、丙三家公司共建一个污水处理站P,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)
作图题:如图,现在甲、乙、丙三家公司共建一个污水处理站P,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论) 如图,在矩形ABCD中,E是AD边上的一点,CE交对角线于点O,△DOE面积为2,△COD面积为8,
如图,在矩形ABCD中,E是AD边上的一点,CE交对角线于点O,△DOE面积为2,△COD面积为8,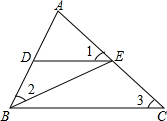 如图所示,∠1=∠2=∠3,请找出所有相似三角形.
如图所示,∠1=∠2=∠3,请找出所有相似三角形.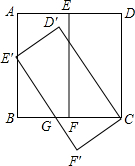 如图,在正方形ABCD中,点E、F分别是AD、BC中点,连接EF,将矩形CDEF绕着点C逆时针旋转一定角度得到矩形CD′E′F′,点E′恰好落在AB边上,E′F′与BC交于点G
如图,在正方形ABCD中,点E、F分别是AD、BC中点,连接EF,将矩形CDEF绕着点C逆时针旋转一定角度得到矩形CD′E′F′,点E′恰好落在AB边上,E′F′与BC交于点G