题目内容
16.如图1,在?ABCD中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.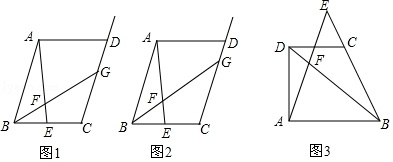
(1)若$\frac{AF}{EF}$=3,求$\frac{CD}{CG}$的值.
(2)如图2,在(1)的条件下,若$\frac{AF}{EF}$=a(a≠0),求$\frac{DG}{AB}$的值(用含a的代数式表示)
(3)如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若$\frac{AB}{CD}$=m,$\frac{BC}{BE}$=n(m>0,n>0),求$\frac{AF}{EF}$的值.(用含m,n的代数式表示).
分析 (1)如图1中,过点E作EH∥AB交BG于点H.由△ABF∽△EHF,推出$\frac{AB}{EH}$=$\frac{AF}{EF}$=3,推出AB=3EH,由四边形ABCD是平行四边形,EH∥AB,推出EH∥CD,AB=CD
又E为BC中点,推出EH为△BCG的中位线,推出CG=2EH,即可推出$\frac{CD}{CG}$=$\frac{AB}{CG}$=$\frac{3EH}{2EH}$=$\frac{3}{2}$.
(2)如图2中,作EH∥AB交BG于点H,则△EFH∽△AFB,推出$\frac{AB}{EH}$=$\frac{AF}{EF}$=a,推出AB=a•EH,由AB=CD,推出CD=a•EH,由EH∥AB∥CD,推出△BEH∽△BCG.推出$\frac{CG}{EH}$=$\frac{BC}{BE}$=2,推出CG=2EH,推出DG=CD-CG=(a-2)EH,由此即可解决问题.
(3)如图3中,过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD.由EH∥CD,推出△BCD∽△BEH,推出$\frac{CD}{EH}$=$\frac{BC}{BE}$=n,推出CD=nEH,又$\frac{AB}{CD}$=m,推出AB=mCD=mnEH,由EH∥AB,推出△ABF∽△EHF,即可推出$\frac{AF}{EF}$=$\frac{AB}{EH}$=mn.
解答 解:(1)如图1中,过点E作EH∥AB交BG于点H.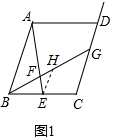
则有△ABF∽△EHF,
∴$\frac{AB}{EH}$=$\frac{AF}{EF}$=3,
∴AB=3EH.
∵四边形ABCD是平行四边形,EH∥AB,
∴EH∥CD,AB=CD,
又∵E为BC中点,
∴EH为△BCG的中位线,
∴CG=2EH,
∴$\frac{CD}{CG}$=$\frac{AB}{CG}$=$\frac{3EH}{2EH}$=$\frac{3}{2}$.
(2)如图2中,作EH∥AB交BG于点H,则△EFH∽△AFB.
∴$\frac{AB}{EH}$=$\frac{AF}{EF}$=a,
∴AB=a•EH,
∵AB=CD,
∴CD=a•EH,
∵EH∥AB∥CD,
∴△BEH∽△BCG,
∴$\frac{CG}{EH}$=$\frac{BC}{BE}$=2,
∴CG=2EH,
∴DG=CD-CG=(a-2)EH,
∴$\frac{DG}{AB}$=$\frac{a-2}{a}$.
(3)如图3中,过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD.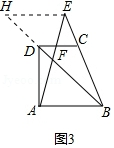
∵EH∥CD,
∴△BCD∽△BEH,
∴$\frac{CD}{EH}$=$\frac{BC}{BE}$=n,
∴CD=nEH,
又$\frac{AB}{CD}$=m,
∴AB=mCD=mnEH,
∵EH∥AB,
∴△ABF∽△EHF,
∴$\frac{AF}{EF}$=$\frac{AB}{EH}$=mn.
点评 本题考查四边形综合题、相似三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形,学会利用参数解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | 6 | B. | 7 | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{7}$ |
 如图△ABC,AB=AC=24厘米,∠B=∠C,BC=16厘米,点D为AB的中点.点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为4或6 厘米/秒.
如图△ABC,AB=AC=24厘米,∠B=∠C,BC=16厘米,点D为AB的中点.点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为4或6 厘米/秒.
 如图,?ABCD对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF.
如图,?ABCD对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF.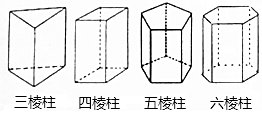 如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.