题目内容
19.在直角三角形中,自锐角顶点所引的两条中线长为$\sqrt{10}$和$\sqrt{35}$,那么这个直角三角形的斜边长为( )| A. | 6 | B. | 7 | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{7}$ |
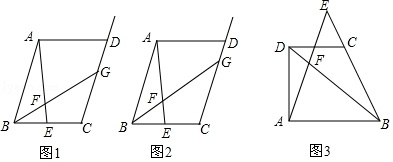
分析 根据题意画出图形,利用勾股定理解答即可.
解答  解:设AC=b,BC=a,分别在直角△ACE与直角△BCD中,根据勾股定理得到:
解:设AC=b,BC=a,分别在直角△ACE与直角△BCD中,根据勾股定理得到:
$\left\{\begin{array}{l}{(\frac{a}{2})^{2}+{b}^{2}=10}\\{{a}^{2}+(\frac{b}{2})^{2}=35}\end{array}\right.$,两式相加得:a2+b2=36,
根据勾股定理得到斜边=$\sqrt{36}$=6.
故选A.
点评 本题是根据勾股定理,把求直角三角形的斜边长的问题转化为求两直角边的平方和的问题.

练习册系列答案
相关题目
10.2016年国家惠农补贴力度将会继续加大,投资者顺应国家政策申报项目,最多能获得1000万元的补贴,用科学记数法表示为( )
| A. | 1.0×105元 | B. | 1.0×106元 | C. | 1.0×107元 | D. | 1.0×108元 |
7.下列几何体中,三视图有两个相同,另一个不同的是( )


| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
4.把一元二次方程x2-4x+1=0,配成(x+p)2=q的形式,则p、q的值是( )
| A. | p=-2,q=5 | B. | p=-2,q=3 | C. | p=2,q=5 | D. | p=2,q=3 |
 完成下面的推理填空
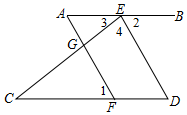
完成下面的推理填空 如图,E是正方形ABCD的BC边上一点,过AE上点P作FG⊥AC,分别交AB、CD于F、G,求证:FG=AE.
如图,E是正方形ABCD的BC边上一点,过AE上点P作FG⊥AC,分别交AB、CD于F、G,求证:FG=AE.