题目内容
8. 如图,?ABCD对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF.
如图,?ABCD对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF.(1)根据题意,补全图形;
(2)求证:BE=DF.
分析 (1)根据要求画出图象即可.
(2)只要证明△BOE≌△DOF(SAS),即可解决问题.
解答 (1)解:图象如图所示.
(2) 证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别是OA,OC的中点,
∴OE=$\frac{1}{2}$OA,OF=$\frac{1}{2}$OC,
∴OE=OF,
在△BOE和△DOF中,
$\left\{\begin{array}{l}{OB=OD}\\{∠BOE=∠DOF}\\{OE=OF}\end{array}\right.$,
∴△BOE≌△DOF(SAS),
∴BE=DF.
点评 本题考查平行四边形的性质、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.方程ax-4y=2y-1是二元一次方程,则a的取值为( )
| A. | a≠0 | B. | a≠-2 | C. | a≠1 | D. | a≠2 |
17.如果反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点(-3,2),则它一定还经过( )
| A. | (-$\frac{1}{2}$,8) | B. | (-3,-2) | C. | ($\frac{1}{2}$,12) | D. | (1,-6) |
18.若(x+2)有平方根,则x的取值范围是( )
| A. | x<-2 | B. | x≤-2 | C. | x>2 | D. | x≥-2 |
 如图,E是正方形ABCD的BC边上一点,过AE上点P作FG⊥AC,分别交AB、CD于F、G,求证:FG=AE.
如图,E是正方形ABCD的BC边上一点,过AE上点P作FG⊥AC,分别交AB、CD于F、G,求证:FG=AE.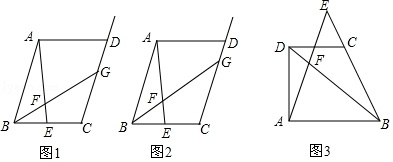
 如图:
如图: