题目内容
16.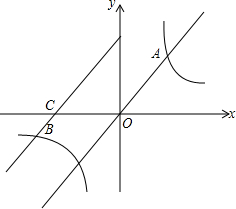 如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A,将直线y=2x向左平移两个单位后与双曲线y=$\frac{k}{x}$的另一分支交于点B,与x轴交于点C,已知$\frac{BC}{OA}$=$\frac{1}{2}$.那么k=32.
如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A,将直线y=2x向左平移两个单位后与双曲线y=$\frac{k}{x}$的另一分支交于点B,与x轴交于点C,已知$\frac{BC}{OA}$=$\frac{1}{2}$.那么k=32.
分析 作AE⊥x轴于E点,BF⊥x轴于F,根据平移得到C点坐标为(2,0),再证明Rt△EOA∽Rt△FCB,利用相似比得到OE=2CF,AE=2BF,设CF=t,则OE=2t,OF=2+t,然后表示A点坐标(2t,4t),B点坐标(-2-t,-2t),再根据反比例函数图象上点的坐标特征得到2t•4t=(-2-t)•(-2t),解得t1=0(舍去),t2=2,于是A点坐标为(4,8),最后把A点坐标代入y=$\frac{k}{x}$即可确定k的值.
解答 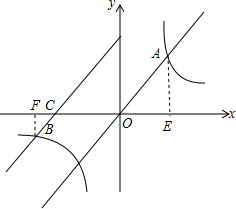 解:作AE⊥x轴于E点,BF⊥x轴于F,如图,
解:作AE⊥x轴于E点,BF⊥x轴于F,如图,
∵直线y=2x向左平移两个单位后得到直线BC,
∴C点坐标为(2,0),
∵OA∥BC,
∴∠AOE=∠BCF,
∴Rt△EOA∽Rt△FCB,
∴$\frac{OA}{BC}$=$\frac{OE}{CF}$=$\frac{AE}{BF}$=2,
∴OE=2CF,AE=2BF,
设CF=t,则OE=2t,OF=2+t,
把x=2t代入y=2x,得y=4t,
即A点坐标为(2t,4t),
∴BF=$\frac{1}{2}$AE=2t,
∴B点坐标为(-2-t,-2t),
∴2t•4t=(-2-t)•(-2t),解得t1=0(舍去),t2=2,
∴A点坐标为(4,8),
把D点坐标代入y=$\frac{k}{x}$得k=4×8=32.
故答案为32.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了相似三角形的判定与性质.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
4.某跳远队准备从甲、乙两名运动员中选去成绩稳定的一名参加比赛,下表是这两名运动员10次测验成绩(单位:m).
你认为应该选择哪名运动员参赛?为什么?
| 甲 | 5.85 | 5.93 | 6.07 | 5.91 | 5.99 |
| 6.13 | 5.98 | 6.05 | 6.00 | 6.19 | |
| 乙 | 6.11 | 6.08 | 5.83 | 5.92 | 5.84 |
| 5.81 | 6.18 | 6.17 | 5.85 | 6.21 |
 如图,∠B=∠C,D在BC上,∠BAD=30°,在AC上取AE=AD,∠ADE=∠AED,求∠EDC的度数.
如图,∠B=∠C,D在BC上,∠BAD=30°,在AC上取AE=AD,∠ADE=∠AED,求∠EDC的度数.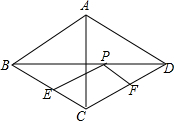 如图,已知菱形ABCD中,对角线AC=12,BD=16,点E、F分别为边BC、CD的中点,点P对角线BD上一动点,则PE+PF的最小值为( )
如图,已知菱形ABCD中,对角线AC=12,BD=16,点E、F分别为边BC、CD的中点,点P对角线BD上一动点,则PE+PF的最小值为( )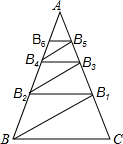 如图,△ABC中,AB=AC=1,∠ABC=72°,BB1平分∠ABC交AC于B1,过B1做B1B2∥BC交AB于B2,作B2B3平分∠AB2B1交AC于B3,过B3作B3B4∥BC交AB于B4,…则线段B1B2的长度为$\frac{3-\sqrt{5}}{2}$,线段B2n-1B2n的长度为($\frac{\sqrt{5}-1}{2}$)n-2.
如图,△ABC中,AB=AC=1,∠ABC=72°,BB1平分∠ABC交AC于B1,过B1做B1B2∥BC交AB于B2,作B2B3平分∠AB2B1交AC于B3,过B3作B3B4∥BC交AB于B4,…则线段B1B2的长度为$\frac{3-\sqrt{5}}{2}$,线段B2n-1B2n的长度为($\frac{\sqrt{5}-1}{2}$)n-2.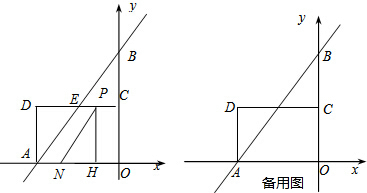
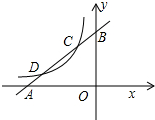 已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线y2=$\frac{k}{x}$(x<0)分别交
已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线y2=$\frac{k}{x}$(x<0)分别交